Uma mistura líquida com molar de etanol e molar água é submetida a uma operação de stripping com vapor de água pura (fluido de arraste) numa col una de estágios com fluxos contra correntes. O produto de fundo da coluna deve conter molar de etanol . A alimentação da m istura líquida encontra -se na temperatura do ponto de bolha (líquido saturado) e a corrente de vapor à saída da coluna é moles por cada mol de alimentação . Para soluções diluí das de etanol - água pode em pregar a seguinte relação de equilíbrio . Quantos estágios ideais são necessários para a separação ?
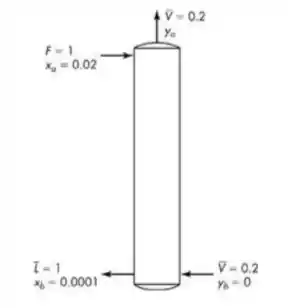
Passo 1
Faaala aíii, tudo show de bola? A coluna dessa questão é similar a uma coluna de absorção, onde a alimentação na forma de vapor entra à base da coluna a solução líquida no topo da coluna.

Onde temos,
E a partir dessas informações vamos calcular o número de estágios com,
Ou,
Passo 2
Como,
Logo,
Para fazer os cálculos vamos supor que:
E,
Passo 3
Calculando o fator de absorção,
Fazendo agora o balanço material da coluna para calcular temos para misturas diluídas,
Substituindo os valores,
Passo 4
Calculando agora o número de estágios necessários temos:
Substituindo os valores temos,
Ou seja, serão necessários estágios.
Repara que você poderia ter usado,
Que o resultado final daria no mesmo, beleza? 😉