A bomba de 28 pol de diâmetro da figura a 1170 rpm é utilizada para bombear água a 20°C através de um sistema de tubulação a 833,3 L/s. (a) Determine a potência de eixo necessária. O fator de atrito médio é 0,018. (b) Se houver 19,8 m de tubo de 300 mm de diâmetro a montante da bomba, a que distância abaixo da superfície deverá ficar a entrada da bomba para evitar cavitação?
Passo 1
Esse exercício envolve o que falamos no tópico anterior (Curvas Características) e o atual (Cavitação). Pode cair assim na prova, então vamos juntos conectar esses conhecimentos 😊
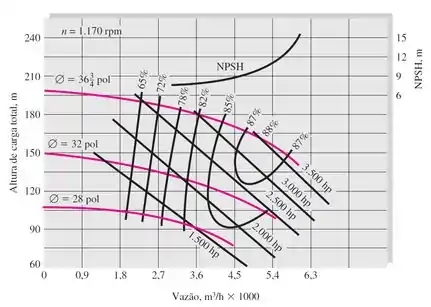
A bomba de 28 polegadas é aquela da curva rosa mais embaixo da figura. A letra (a) do exercício pede a potência dessa bomba quando a vazão é 833,3 L/s.
A potência de eixo , como vimos na teoria de Curvas Características, pode ser calculada assim:
Além disso, a potência da bomba é essa aqui:
Então, a potência de eixo que queremos calcular é:
Do enunciado, sabemos que:
e estão no Sistema Internacional, falta converter a vazão volumétrica
Além disso, na figura, o eixo x é a vazão volumétrica em
Encontrando essa vazão na curva da bomba escolhida na figura, conseguimos encontrar a carga da bomba e a eficiência! Repara só:
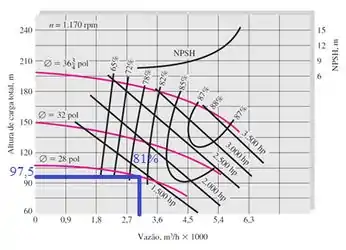
Pelo gráfico, encontramos os valores aproximados e . Encontramos 81% de eficiência, pois o ponto de operação se encontra entre as curvas de eficiência de 78% e 82%, estando mais próxima da segunda 😉 Mas é uma aproximação mesmo, você pode considerar outro valor próximo disso aí.
Substituindo os valores (no Sistema Internacional) na potência de eixo:
A potência de eixo é
Passo 2
Na letra b, o exercício pergunta qual seria a distância que a bomba deve ficar abaixo da superfície para não cavitar. Falou em cavitação, lembrou de NPSH. Mas como vamos calcular ele?
Pela fórmula:
Mas o enunciado não deu a velocidade média de entrada e nós não conhecemos .
“E agora, José?”
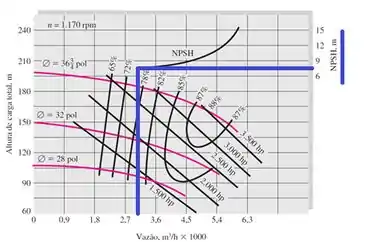
A resposta está na figura. Na vertical, do lado direito, olha só quem tá lá. Sim! A NPSH! =D UHUL! E na vazão ,
Passo 3
Agora que já sabemos o NPSH, vamos lembrar do objetivo do exercício: encontrar a distância abaixo da superfície que a bomba deve ficar para não cavitar.
O nosso volume de controle vai da superfície submetida a pressão atmosférica (1) até a entrada da bomba (2).
Como o início do percurso é a superfície, e essa é nossa referência, então e (na superfície, consideramos que a velocidade é nula pois a área é muito grande).
Além disso, não tem turbina e a bomba em si não está incluída do volume de controle (o VC vai até a entrada da bomba, onde não ocorreu a transferência de energia). Com isso nesse VC
Opa! Não conhecemos e (pressão e velocidade na entrada da bomba). Fica tranquilo, pois é aqui que o NPSH vai nos ajudar.
Na equação de energia, a gente vai adicionar e subtrair o mesmo termo, então não vamos modificar nada.
Mas assim o nosso NPSHD apareceu:
A partir de agora, vamos resolver essa equação aos poucos para encontrar o , que é a posição da entrada da bomba em relação à superfície.
Conhecemos ,
Além disso, pelas propriedades da água a 20°C, e
Substituindo na equação da energia
Simplificando
Vamos calcular a perda de carga agora. A perda que ocorre é a perda de carga global, calculada por essa equação:
Do enunciado, sabemos que . Para calcular V, vamos utilizar a vazão e a área do tubo nessa região (diâmetro = 300 mm = 0,3 m)
Substituindo
Finalmente na equação da energia
É isso aí! Por que esse sinal negativo? Pois a bomba deve ficar 5,8 m abaixo da superfície para evitar cavitação.
Resposta
a)
b) A bomba deve ficar 5,8 m abaixo da superfície para evitar cavitação.