Uma amostra de gás se expande de e para e seguindo a trajetória do diagrama da figura abaixo. Em seguida, o gás é comprimido de volta para , seguindo a trajetória ou a trajetória . Calcule o trabalho líquido realizado pelo gás para o ciclo completo ao longo da trajetória e da trajetória .
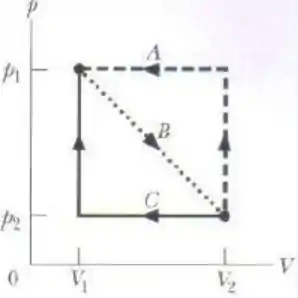
Passo 1
Opa, e ai belezinha? Bora para mais uma questão sobre ciclos!!
Antes de botar a mão na massa vamos lembrar de algumas coisinhas:
- O trabalho de um ciclo é igual a área interna do seu gráfico.
- Sentido for horário Trabalho positivo
- Sentido anti-horário Tranalho negativo.
Agora vamos ver o que é pedido
Então para calcular o trabalho do ciclo vamos fazer a área desse triângulo
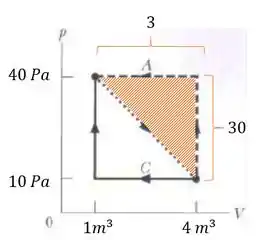
A área do triângulo retângulo é calculada assim:
Substituindo os valores que coloquei no gráfico da base e da altura do triângulo, temos
Fazendo essa continha encontramos
Como o sentido é anti-horário o trabalho é negativo assim
Passo 2
Faremos o mesmo para o triângulo
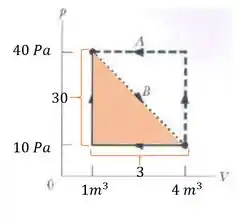
Calculando a área desse triângulo, temos
Como nesse caso o sentido é horário, o trabalho é positivo