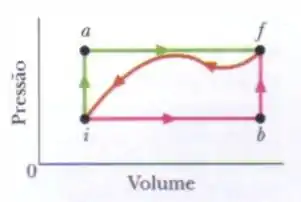
Quando um sistema passa do estado para o ao longo da trajetória da figura abaixo, . . Ao longo da trajetória , .
Dados: e
Se , qual o valor de ? Se , qual o valor de :
Na trajetória ?
Na trajetória
Passo 1
Faaala aí! Vamos pra mais uma questão sobre Ciclos e a primeira lei da termodinâmica!
Bom, o enunciado quer o valor de em duas situações, para isso precisamos achar primeiro a variação de energia interna na trajetória , para isso vamos achar .
Como o é a variação da energia interna, então calculamos como sendo a energia interna final menos a inicial
Beleza, já sabemos que
Mas não temos as outras informações ☹
Relaxa, podemos encontrar o lembrando que a variação da energia interna só depende da posição inicial e final, não importa o caminho. Então podemos dizer que
Como o enunciado já nos deu
Então teremos
Substituindo na equação alí de cima, teremos
Passando o para o outro lado, ele vai positivo
Logo
Passo 2
Show, agora podemos partir para a letra
Tendo o valor da energia interna no ponto e no ponto , podemos calcular a variação da energia interna e aplicar a primeira lei entre os dois pontos.
O enunciado dá os valores de
Então fica tranquilinho calcular o
Substituindo
Show! Como o enunciado pede o , precisamos usar a primeira lei da termodinâmica
Substituindo o valor que encontramos
Precisamos dar uma analisada no gráfico agora.
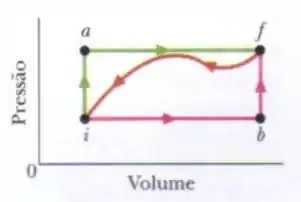
Repare que na trajetória primeiro temos um aumento de volume de para e depois o volume não é alterado de para . Então podemos dizer que houve trabalho de para , mas não houve de para .
Como o trabalho de pode ser dividido em duas partes
Então
E já foi dado no enunciado o valor do trabalho de para
Voltando para nossa equação
Agora substituindo o que acabamos de calcular
Podemos passar o para o outro lado positivo
E finalmente
Passo 3
Belezinha, vamos pra letra Na trajetória
Vamos fazer a mesma coisa que antes:
No passo encontramos e o enunciado nos fornece
Pela primeira lei da termodinâmica, temos que
Como temos uma transformação isovolumétrica o trabalho vale zero!
a equação fica:
Resposta
O valor de