Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 7.Perguntas e Problemas - Ex. 41
Uma amostra de latão que não foi trabalhada a frio, com tamanho médio de grão de , possui um limite de escoamento . Estime o limite de escoamento para essa liga após ela ter sido aquecida a durante . O valor de é conhecido e vale .
Passo 1
Para resolvermos essa questão vamos utilizar a questão que é dada pro
Desejamos descobrir o valor de , mas precisamos descobrir o valor de tendo em vista que a nossa amostra foi aquecida por na figura conseguimos encontrar o valor desse diâmetro para fazendo aproximações
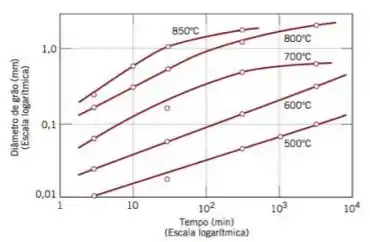
Temos que após o tamanho do grão será aproximadamente . Pronto, temos tudo para resolver nosso problema basta substituirmos nossos dados na equação e, assim, encontramos
Que é exatamente o que o exercício deseja.
Resposta
Exercícios de Livros Relacionados
O diâmetro médio de grão para um latão foi medido em função do tempo a 650 ° C , o que está mostrado na tabela a seguir para dois tempos diferentes: a Qual era o diâmetro original de grão? b Qual seri
a A partir da figura 7.25 , calcule o tempo necessário para que o diâmetro médio de grão aumente de 0,01 para 0,1 m m a 500 ° C , para o latão. b Repita o cálculo para 600 ° C .
É necessário selecionar uma liga metálica para uma aplicação que requer um limite de escoamento de pelo menos 345M P a50000p s i , ao mesmo tempo em que se mantém uma ductilidade mínima % A L de 20 %
Um corpo de provas cilíndrico de aço trabalhado a frio possui uma dureza Brinell de 250 . a Estime sua ductilidade em termos dos alongamentos percentual. b Se o corpo de provas permaneceu cilíndrico d
Determine se é possível trabalhar a frio um aço para obter uma dureza Brinell mínima de 225 e, ao mesmo tempo, ter uma ductilidade de pelo menos 12 % A L . Justifique sua decisão.