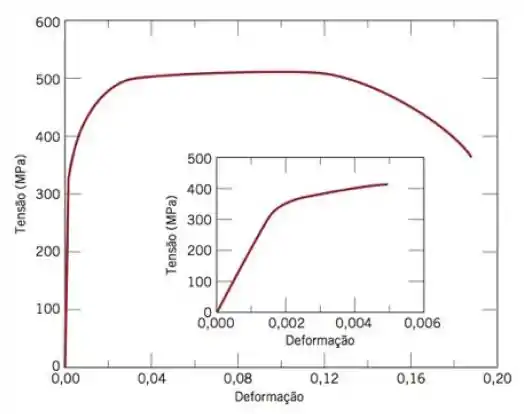
Uma barra de aço, que exibe o comportamento tensão-deformação mostrado na Figura 6.21, é submetida a uma carga de tração; o corpo de provas possui 300mm (12in) de comprimento e uma seção transversal quadrada com 4.5mm (0.175) de lado.

1. Calcule a magnitude da carga necessária para produzir um alongamento de 0.45mm (0.018in).
2. Qual será a deformação após a carga ter sido liberada?

A figura 6.21 é:

Letra a:

Pede-se que calculemos a magnitude da carga necessária para produzir um alongamento de 0,45 mm para o aço, exibindo o comportamento de tensão-deformação mostrado na Figura 6.21. Primeiro, calcule a tensão e, em seguida, a tensão correspondente da plotagem.

Isso está próximo do fim da região elástica; da inserção da Figura 6.21, isso corresponde a uma tensão de cerca de 300 MPa (43.500 psi). Agora, da Equação 6.1

em que b é o comprimento lateral da seção transversal. Portanto