Um corpo de provas de ferro fundido maleável, tendo uma seção transversal retangular com dimensões de 4.8mm 15.9mm (3/16in 5/8in) é deformado em tração. Usando os dados carga-alongamento mostrados na tabela a seguir, complete os itens (a) a (f).
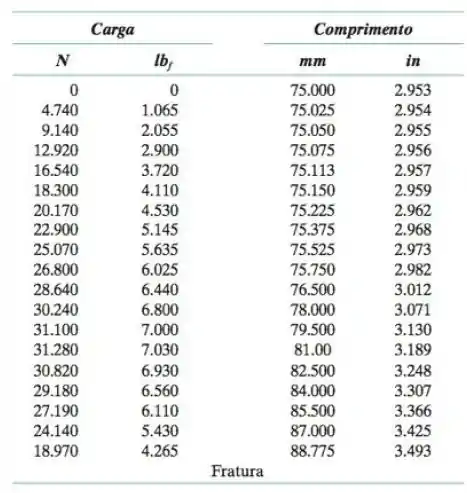
- Represente graficamente os dados da tensão de engenharia em função da deformação de engenharia.
- Calcule o módulo de elasticidade.
- Determine o limite de escoamento para uma pré-deformação de 0.002.
- Determine o limite de resistência à tração para essa liga.
- Calcule o módulo de resiliência.
- Qual é a ductilidade em termos do alongamento percentual?
Passo 1
Esse problema exige que façamos um gráfico de tensão-deformação para um ferro fundido dúctil, dados seus dados de comprimento de carga de tração e, em seguida, determinemos algumas de suas características mecânicas.
Na letra a:
Os dados são plotados abaixo em dois gráficos: o primeiro corresponde a toda a curva de tensão-deformação, enquanto que, no segundo, a curva se estende um pouco além da região elástica da deformação.
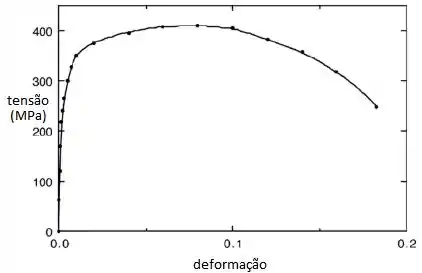
Passo 2
Na letra b:
O módulo de elasticidade é a inclinação na região elástica linear (Equação 6.10) como
Passo 3
Na letra c:
Para a força de escoamento, a linha de compensação de deformação de 0,002 é desenhada tracejada. Ele cruza a curva tensão-deformação a aproximadamente 280 MPa (40.500 psi).
Passo 4
Na letra d:
A resistência à tração é de aproximadamente 410 MPa (59.500 psi), correspondendo à tensão máxima no gráfico de tensão-deformação completo.
Passo 5
Na letra e:
Da Equação 6.14, o módulo de resiliência é apenas
que, usando os dados computados acima, gera um valor de
Passo 6
E, finalmente, na letra f:
A ductilidade, em percentagem de alongamento, é apenas a deformação plástica na fratura, multiplicada por cem. A tensão total da fratura na fratura é de 0,185; subtrair a tensão elástica (que é cerca de 0,001) nos deixa com uma tensão plástica de 0,184. Assim, a ductilidade é de cerca de 18,4% EL.
Resposta
-
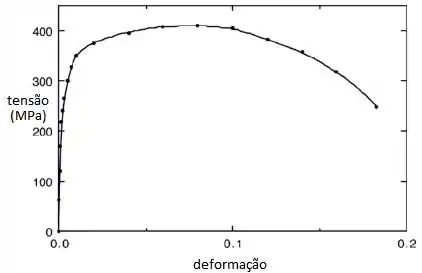
- Ele cruza a curva tensão-deformação a aproximadamente 280 MPa (40.500 psi).
- A resistência à tração é de aproximadamente 410 MPa (59.500 psi), correspondendo à tensão máxima no gráfico de tensão-deformação completo.
- A ductilidade é de cerca de 18,4% EL.