Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 12
Como observado na Seção 3.15, as propriedades físicas dos monocristais de algumas substâncias são anisotrópicas; isto é, elas são dependentes da direção cristalográfica. Uma dessas propriedades é o módulo de elasticidade. Para os monocristais cúbicos, o módulo de elasticidade em uma direção genérica , , é descrito pela relação
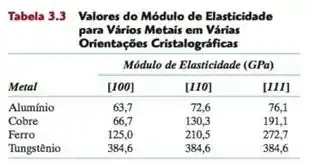
Em que e são os módulos de elasticidade nas direções e , respectivamente; , e são cossenos dos ângulos entre e as respectivas direções e . Verifique se os valores de para o alumínio, o cobre e o ferro na tabela 3.3 estão corretos.
Passo 1
Pra resolver essa questão a gente vai usar a fórmula que foi dada no enunciado, mas pra isso vamos precisar do valores de e , e também de , e . Os dois primeiros a gente vai conseguir ver naquela tabela que o enunciado falou (tabela 3.3), mas os outros a gente vai ter que pensar através da estrutura cristalina de cada um.
Passo 2
Os 3 metais tem estrutura cúbica. Então vamos ver os valores dos ângulos pra cada um.
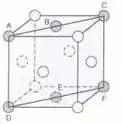
Na estrutura CFC, vemos que o ângulo entre a direção mostrado na figura e (perpendicular ao eixo x) é . O ângulo com a direção (perpendicular ao eixo y) também é . Agora, o ângulo com a direção é
Os cossenos vão ser então:
Passo 3
Agora vamos calcular o valor pros 3 usando os dados que encontramos!
Fazendo as contas pro Alumínio, encontramos que:
Para o Cobre temos que:
Para o Ferro temos que:
Como podemos ver os valores da tabela estão suficientemente próximos para serem considerados corretos!
Resposta
Os valores da tabela estão corretos!