Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 15
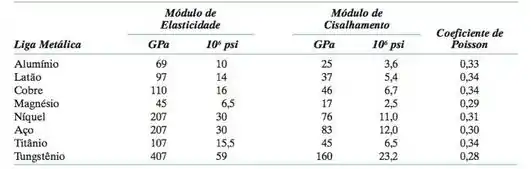
Um corpo de provas cilíndrico de alumínio tendo uma diâmetro de 19 mm (0,75 in) e um comprimento de 200 mm (8,0 in) é deformado elasticamente em tração com uma força de 48.800 N (11.000 lbf). Considerando os dados da tabela, determine o seguinte:
- Quanto esse corpo de provas irá se alongar na direção da tensão aplicada.
- A variação no diâmetro do corpo de provas. O diâmetro irá aumentar ou diminuir?
Passo 1
Pra resolver essa a letra a, a gente vai usar a fórmula que descreve o gráfico da deformação elástica:
Lembrando que o gráfico é linear, então a tensão é proporcional à deformação , e o que dita a relação é o módulo de elasticidade E, que é o que a gente quer.
Mas primeiro, temos que passar essa carga que foi dada no enunciado para termos de tensão:
Além disso, para encontrar esse alongamento temos que saber a expressão da deformação:
Onde é o comprimento inicial e é então o alongamento real.
Uma coisa de cada vez! Vamos começar com a tensão!
Passo 2
Calculando a tensão:
Agora calculando a deformação:
Pra isso a gente precisa saber o módulo de elasticidade do Alumínio. Na tabela que a questão deu temos que: .
Passo 3
Finalmente, agora vamos calcular o alongamento! Rearranjando a fórmula temos que:
Passo 4
Pra resolver a letra b, precisamos pensar no que que está acontecendo com o corpo de provas. Se o ensaio é de tração, significa que o corpo está sendo esticado, ou seja, o comprimento aumenta.
Como a massa e, consequentemente, o volume não pode mudar pelo princípio de conservação de massa, então o diâmetro só pode diminuir!
Resposta
- Diminuir