Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 10

Considere um corpo de provas cilíndrico feito de aço com 10,0 mm (0,39 in) de diâmetro e 75 mm (3,0 in) de comprimento, puxado em tração. Determina seu alongamento quando uma carga de 20.000 N (4.500 lbf) é aplicada.

Passo 1

Pra resolver essa questão, primeiro vamos ter que passar essa carga que foi dada no enunciado para termos de tensão:

σ = F A

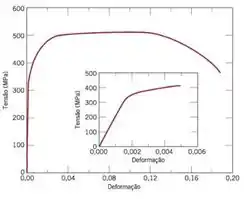
Com o valor da tensão poderemos olhar a deformação no gráfico. Após encontrar a deformação podemos encontrar o alongamento usando a expressão da deformação:

ε = ( I - I 0 ) I 0

Onde I 0 é o comprimento inicial e ( I - I 0 ) é o alongamento.

Uma coisa de cada vez! Vamos começar calculando a tensão!

Passo 2

Calculando a tensão:

σ = F A = F π D ² 4 = 20 . 000 π ( 0,010 ) ² 4 = 254.647.908,9   P a =   254,65   M P a

Agora precisamos olhar o valor da deformação ε , para esse valor de tensão σ no gráfico!

Passo 3

Eu encontrei ε = 0,0015 , mas não tem problema se você encontrou alguma coisa um pouco diferente!

Diga: Um outro jeito de calcular seria usar o gráfico para calcular o módulo de elasticidade e com ele calcular a deformação através da relação σ = E   x   ε . Daria mais trabalho, mas daria certo também!

Vamos então finalmente calcular o alongamento:

ε = ( I - I 0 ) I 0

I - I 0 = 0,0015   x   75 = 0,1125   m m  

Resposta

I - I 0 = 0,1125   m m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um corpo de provas cilíndrico de uma liga metálica hipotética é tensionado em compressão. E seus diâmetros original e final são 20,000 e 20,025 mm, respectivamente, e o seu comprimento final é 74,96 m
Uma barra cilíndrica em aço com 10 mm (0,4 in) de diâmetro deve ser deformada elasticamente pela aplicação de uma força ao longo do seu eixo. Aplicando os dados da tabela, determine a força que produz
Um corpo de provas metálico de formato cilíndrico e com 12,7 mm (0,5 in) de diâmetro e 250 mm (20 in) de comprimento deve ser submetido a um tensão de tração de 28 Mpa (4.000 psi). Nesse nível de tens
Considere a liga de latão para a qual o comportamento tensão-deformação está mostrado na figura. Um corpo de provas cilíndrico desse material com 6mm (0,24 in) de diâmetro e 50 mm (2 in) de compriment
Uma barra cilíndrica com 380 mm (15,0 in) de comprimento e diâmetro de 10,0 mm (0,40 in) deve ser submetida a uma carga de tração. Se a barra não deve sofrer deformação plástica ou um alongamento de m