Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 16
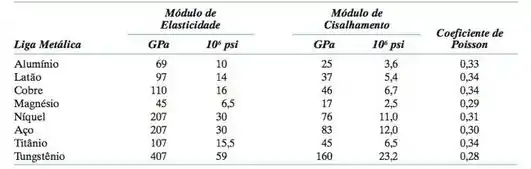
Uma barra cilíndrica em aço com 10 mm (0,4 in) de diâmetro deve ser deformada elasticamente pela aplicação de uma força ao longo do seu eixo. Aplicando os dados da tabela, determine a força que produzirá uma redução elástica de () no diâmetro.
Passo 1
Pra resolver essa questão, primeiro a gente vai precisar relacionar a deformação lateral (do diâmetro) e a deformação axial (do comprimento). Pra isso a gente usa o coeficiente de Poisson :
Pra chegar no coeficiente de Poisson, a gente usa a expressão:
Mas antes de tudo, para chegar nessa relação temos que saber a expressão da deformação:
Depois disso podemos usar a fórmula que descreve o gráfico da deformação elástica:
E por fim, passar essa carga que foi encontrada para termos de tensão:
Passo 2
Primeiro, vamos calcular o coeficiente de Poisson pro aço:
Precisamos também encontrar a deformação lateral:
Agora temos tudo que precisamos pra calcular a deformação axial:
Passo 3
Agora que temos a deformação, podemos calcular a tensão e por fim a carga:
Finalmente, agora vamos calcular a carga!