Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 15.Perguntas e Problemas - Ex. 2

Calcule os módulos elásticos para os seguintes polímeros

  1. Polietileno de alta densidade
  2. Náilon
  3. Fenol-formaldeído (baquelite)

Como esses valores se comparam com os apresentados na Tabela 15.1 para os mesmos polímeros?

Passo 1

E ai galerinha do meu Brasil, para calcularmos o módulo de elasticidade dos materiais, temos que usar a equação ali embaixo. Vamos considerar a tensão e deformação inicial dos materiais igual a zero ok? Partindo do pressuposto que eles ainda não foram ensaiados então não ocorreu nenhuma tensão e deformação no material.

Com isso partiu calcularmos?

  1. Vamos considerar uma tensão na região elástica de 6MPa e uma deformação de aproximadamente 0,002

    2. E   = 20,5 M P a - 0 0,006 - 0

    E   = 3,41   G P a  

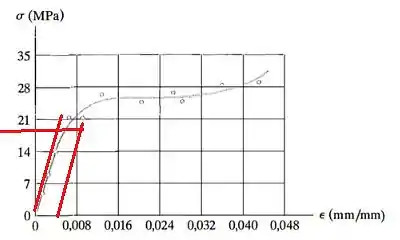
    O módulo de elasticidade (médio) para o PEAD apresentado na Tabela 15.1 é de 1,08 GPa, que significativamente menor que esse valor.

    Passo 2

  2. Galera agora faremos para o náilon seguindo a mesma lógica da alternativa anterior

    3. E   = 23,8   M P a - 0 M P a 0,008 - 0

    E = 2,97 G P a  

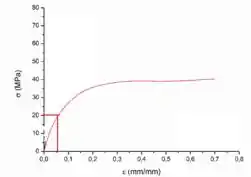
    A faixa do módulo de elasticidade para o nylon é de 1,58 GPa a 3,80 GPa; portanto, o valor para o nylon está dentro dessa faixa.

    Passo 3

  3. Galera e por último e não menos importante, o baquelite :D

E   = 31 M P a - 0 M P a 0,065 - 0

E   = 4,76   G P a

O intervalo do módulo de elasticidade para o baquelite apresentado na Tabela 15.1 é de 2,76 GPa a 4,83 Gpa, entretanto nosso valor está nessa faixa :D

Resposta

  1. E   = 3,41   G P a  
  2. E = 2,97 G P a  
  3. E   = 4,76   G P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra, para um ferro fundido cinzento, a curva tensão-deformação de engenharia em tração na região elástica. Dertemine (a) o módulo tangente tomado a 10,3 Mpa (1500 psi) e (b) o módulo secan
Uma barra cilíndrica feita de cobre (E=110 GPa, 16 x 10 6 psi), que possui um limite de escoamento de 240 Mpa (35.000 psi), deve ser submetida a uma carga de 6660N (1500 lbf). Se o comprimento da barr
Considere um arame cilíndrico de titânio com 3,0 mm (0,12 in) de diâmetro e 2,5 x 10 4 mm (1000 in) de comprimento. Calcule seu alongamento quando uma carga de 500 N (112 lbf) é aplicada. Assuma que a
Considere um corpo de provas cilíndrico feito de aço com 10,0 mm (0,39 in) de diâmetro e 75 mm (3,0 in) de comprimento, puxado em tração. Determina seu alongamento quando uma carga de 20.000 N (4.500
Como observado na Seção 3.15, as propriedades físicas dos monocristais de algumas substâncias são anisotrópicas; isto é, elas são dependentes da direção cristalográfica. Uma dessas propriedades é o mó