Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 12.Perguntas e Problemas - Ex. 7
Calcule o fator de empacotamento atômico para a estrutura cristalina do cloreto de césio, para a qual .
Passo 1
O problema nos pede para calcularmos o fator de empacotamento atômico para o composto dado com a sua respectiva relação entre os raios do cátion e do ânion. Pois bem, a equação que vamos precisar para resolver esse problema é dada no capítulo do livro a qual podemos escrever como sendo
Vamos denotar aqui o volume dos átomos em uma célula unitária como sendo e o volume total da célular unitária como sendo . Além disso, adotaremos que nossos átomos são esferas rígidas. Sendo assim, pela tabela temos que a estrutura cristalina do Cloreto de Césio é cúbica simples com na qual o interstício cúbico é ocupado pelo ânion , então, por célula unitária teremos 1 esfera catiônica e 1 aniônicas, dessa forma nosso fica sendo
Como temos vamos encontrar
Passo 2
Pois bem, precisamos agora calcular nosso volume total que é dado por
Precisamos achar uma relação entre o lado do cubo e nossos raios do cátion e ânion, dessa forma tomemos um modelo de célula unitária simplificado onde teremos
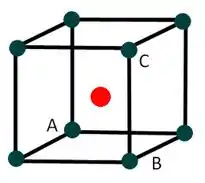
Temos que a diagonal do nosso cubo de lado é dada por e ainda temos que ela vale , assim, igualando essa equações temos
Então teremos
Então, finalmente, nosso fator de empacotamento será dado por