Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 32

Determine os índices para as direções mostradas na seguinte célula unitária cúbica:

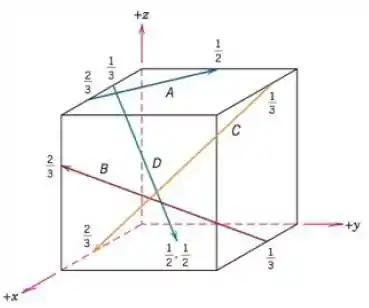
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos trazer o desenho do enunciado para cá pra melhorar a visualização:

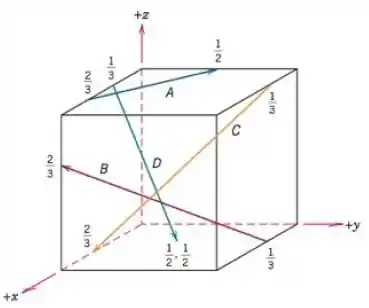
Para determinar os índices para as direções, temos a seguinte regra:

í n d i c e = c o o r d e n a d a s   d o   f i n a l - c o o r d e n a d a s   d a   o r i g e m

Como a célula unitária é cúbica, temos que:

a = b = c = 1

Passo 2

A partir das considerações do passo anterior, podemos descobrir os índices para as direções. Temos que:

Direção A :

í n d i c e = 0   1 2   1 - 2 3   0   1

í n d i c e = 0 - 2 3   1 2 - 0   1 - 1

Temos, portanto:

í n d i c e = 2 3 -   1 2   0

Ou:

4 -   3   0

Direção B :

í n d i c e = 1   0   2 3 - 1 3   1   0

í n d i c e = 1 - 1 3   0 - 1   2 3 - 0

Temos, portanto:

í n d i c e = 2 3   1 -   2 3

Ou:

2   3 -   2

Passo 3

Direção C :

í n d i c e = 2 3   0   0 - 1 3     1   1

í n d i c e = 2 3 - 1 3   0 - 1   0 - 1

Temos, portanto:

í n d i c e = 1 3     1 -   1 -

Ou:

1   3 -   3 -

Direção D :

í n d i c e = 1 2     1 2   0 - 1 3     0     1

í n d i c e = 1 2 - 1 3   1 2 - 0   0 - 1

Temos, portanto:

í n d i c e = 1 6     1 2   1 -

Ou:

1   3   6 -

Resposta

Direção A : 4 -   3   0

Direção B : 2   3 -   2

Direção C : 1   3 -   3 -

Direção D : 1   3   6 -

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você esperaria que ao solidificar, um material no qual as ligações atômicas são predominantemente iônicas tenha maior ou menor probabilidade de formar um sólido não cristalino em comparação a um mater
A figura 3.25 mostra os quatros primeiros picos do difratograma de raios x para o cobre, que possui uma estrutura cristalina CFC, foi usada radiação x monocromática com comprimento de onda de 0,1542 n
Se o raio atômico do alumínio é de 0,143 nm, calcule o volume da sua célula unitária em metros cúbicos.
Mostre que para a estrutura cristalina cúbica de corpo centrado o comprimento da aresta da célula unitária a e o raio R estão relacionados por a =4 R 3 .
Mostre que a razão ideal c / a ideal é de 1,633, para a estrutura cristalina HC.