Calcule o módulo de elasticidade para as seguintes ligas metálicas: (a) titânio, (b) aço revenido, (c) alumínio e (d) aço carbono. Como esses valores se compara àqueles apresentados na Tabela 6.1 para os mesmos materiais?
Passo 1
Pra resolver essa questão, a gente vai precisar usar a fórmula que descreve o gráfico da deformação elástica:
Além disso, para encontrar a deformação através do alongamento dado, temos que saber a expressão da deformação:
Onde é o comprimento inicial e é então o alongamento.
Passo 2
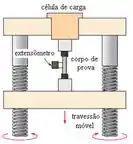
Como o livro indica lá no comecinho, para resolver essa questão é necessário o recurso de ensaios de tração! Ele mostra disso através da figurinha que está do lado do enunciado

Como a gente não tem todos esses materiais disponíveis para os ensaios, vou contar pra você direitinho como você teria que fazer, beleza?
Passo 3
Você precisaria pegar uma amostra cilíndrica ou uma barra pra cada material e anotar o comprimento inicial. Com isso você tem que fazer o ensaio de tração (que estica a amostra) aplicando diferentes forças.
Quanto mais pontos melhor! E a cada tração você deve anotar o novo comprimento da amostra.
Com todos esses dados você calcula o alongamento adimensional da fórmula lá do passo 1 e monta um gráfico tensão x deformação. À partir desse gráfico você calcular o módulo de elasticidade como o coeficiente linear da parte reta do gráfico!
Resposta
Não temos resposta, mas temos um desafio