Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 56
- Desenvolva expressões para a densidade planar em termos do raio atômico R para as direções (0001) na estrutura HC.
- Calcule o valor da densidade planar para esse mesmo plano no magnésio.
Passo 1
Letra a:
Um plano (0001) para uma célula de unidade HC é mostrado abaixo:
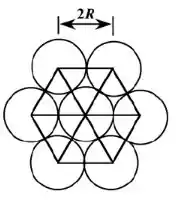
Cada um dos 6 átomos de perímetro nesse plano é compartilhado com outras três células unitárias, enquanto o átomo central não é compartilhado com nenhuma outra célula unitária; isso dá origem a três átomos equivalentes pertencentes a este plano.
Em termos do raio atômico R, a área de cada um dos 6 triângulos equilaterais que foram desenhados é , ou a área total do plano mostrado é . E a densidade planar para este plano (0001) é igual a:
Passo 2
Na letra b:
Da tabela do livro, o raio atômico do magnésio é de 0,160 nm. Portanto, a densidade planar para o plano (0001) é:
Resposta
Exercícios de Livros Relacionados
Desenhe uma célula unitária ortorrômbica e no interior dessa célula um plano 210 .Desenhe uma célula unitária monoclínica e no interior dessa célula um plano 002 .
Considerando as Equações 3.6 a , 3.6 b , 3.6 c e 3.6 d , desenvolva expressões para cada um dos três conjuntos de índices “linha” u ' ,v ' ew ' em termos dos quatro índices “sem linha” u , v , tew .
Quais são os índices para os dois planos representados no desenho a seguir?
Determine os índices de Miller para os planos mostrados na seguinte célula unitária:
Esboce em uma célula unitária cúbica os seguintes planos: 0 1 - 1 - 11 2 - 10 2 - 1 3 - 1 1 - 1 1 - 1 2 - 2 - 1 - 2 3 - 0 1 - 3 -