Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 3
Mostre que para a estrutura cristalina cúbica de corpo centrado o comprimento da aresta da célula unitária e o raio estão relacionados por .
Passo 1
Pra resolver essa questão, um bom jeito de começar é desenhando a estrutura cristalina e visualizando aonde os átomos se encostam dentro da célula unitária.
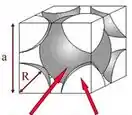
No desenho a gente pode ver que o átomo do meio encosta nos átomos das pontas. Sendo assim, se a gente traçar a diagonal do cubo obtemos a relação entre a diagonal e o total de 4 raios.
Já que da geometria já é conhecido que a diagonal do cubo vale a aresta do cubo vezes . Temos a seguinte relação:
Passo 2
Rearranjando os termos da igualdade, obtemos que:
Resposta
, como queríamos demonstrar!
Exercícios de Livros Relacionados
Usando os raios iônicos da Tabela 12.3, calcule a massa específica teórica do CsCl. (Sugestão: use uma modificação do resultado do Problema 3.3).A massa específica medida é de 3.99 g / c m 3 . Como vo
Calcule a massa específica teórica do Z n S dado que a distância Z n - S e o ângulo de ligação são de 0.234 n m e 109.5 º º, respectivamente. Como esse valor se compara à massa específica medida?
A célula unitária para o M g F e 2 O 4 ( M g O - F e 2 O 3 ) apresenta simetria cúbica com comprimento da aresta da célula unitária de 0.836 n m . Se a massa específica desse material é de 4.52 g / c
Sabe-se que um material cerâmico hipotético do tipo AX tem massa específica de 2,65 g / c m 3 e uma célula unitária com simetria cúbica e comprimento da aresta de 0,43 nm. Os pesos atômicos dos elevam
Calcule o fator de empacotamento atômico para o cloreto de césio usando os raios iônicos da Tabela 12.3 e assumindo que os íons tocam-se ao longo das diagonais do cubo.