O zircônio possui uma estrutura cristalina HC e uma massa específica de
- Qual é o volume da sua célula unitária em metros cúbicos?
- Se a razão é de 1,593, calcule os valores de c e de a.
Passo 1
Na letra a, pra calcular o volume da célula unitária, primeiro vamos ter que saber quantos átomos existem dentro de uma célula unitária e, através do seu peso atômico, calcular a massa em uma célula. À partir daí usamos a massa específica para chegar no valor do volume.
Na letra b, tendo o valor do volume e a relação entre c e a, podemos usar a fórmula do volume do prisma hexagonal para calcular os tais valores.Primeiro de tudo então, vamos olhar aqui pra essa figura pra ver quantos átomos tem nesse célula unitária:
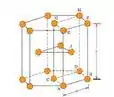
O número de átomos dentro da célula unitária é átomos! Bora calcular o resto!
Passo 2
Para calcular a massa dentro da célula unitária, primeiro precisaremos saber o peso atômico do zircônio. Consultando a tabela periódica mais perto de você temos que Também precisaremos usar a relação de Avogadro que diz que em 1 mol de moléculas existem partículas!
Como temos 6 átomos em uma célula:
Agora vamos calcular o volume!Em metros cúbicos:
Passo 3
Agora vamos calcular c e a, sabendo que , ou seja, .
A fórmula do volume do prisma hexagona é igual a área do hexágono vezes a altura:
Como já temos o valor do volume, a gente só precisa igualar! Mas antes, vamos converter as unidades! Finalmente, encontrando a:
Agora ficou fácil achar c!
Resposta
- e