Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 50

Determine os índices para os planos mostrados nas seguintes células unitárias hexagonais:

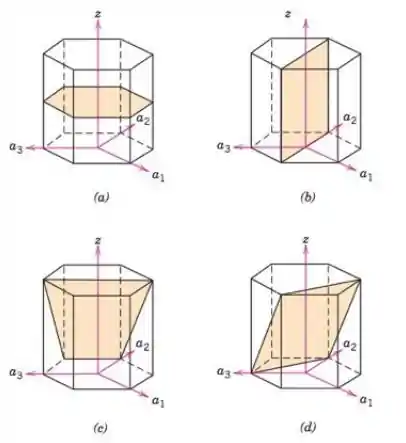
Passo 1

Na letra a:

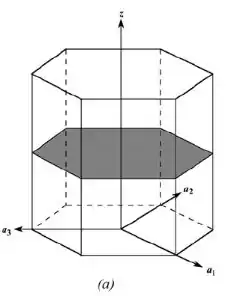
Para esse plano, as interseções com os eixos a 1 ,   a 2 e z são ∞ a ,   ∞ a e c 2 (o plano é paralelo aos eixos a 1   e   a 2 . Em termos de a e c, essas interseções são ∞ ,   ∞ e 1 2 , cujos respectivos recíprocos são 0, 0 e 2. Isso significa que:

h = 0

k = 0

l = 2

Agora, a partir da Equação 3.7, o valor de i é

i =   - ( h + k ) =   - [ 0 + 0 ] = 0

Portanto, este é um plano (0002).

Passo 2

Na letra b:

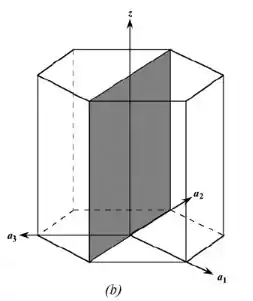
Este plano passa pela origem do sistema de eixos coordenados; portanto, convertemos esse plano em uma unidade de distância ao longo do eixo x, conforme o esboço mostrado abaixo:

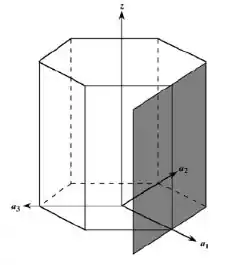
Nesse ponto, o plano cruza os eixos a 1 ,   a 2 e z em a ,   ∞ a ,   ∞ c respectivamente (o plano é paralelo aos eixos a 2 e z ). Em termos de a e c, essas interseções são 1 ,   ∞   e   ∞ cujos respectivos recíprocos são 1, 0 e 0. Isso significa que:

h = 1

k = 0

l = 0

Da Equação 3.7, o valor de i é:

i =   - ( h + k ) =   - ( 1 + 0 ) =   - 1

Então, é um plano ( 10 1 _ 0 ) .

Passo 3

Na letra c:

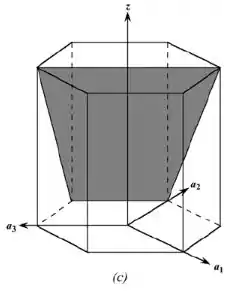
Para esse plano, as interseções com os eixos a 1 ,   a 2   e   z são –a, a e c. Em termos de a e c, essas interseções são -1, 1 e 1, cujos respectivos recíprocos são 0, 1 e 1. Isso significa que:

h =   - 1

k = 1

l = 1

Da Equação 3.7, o valor de i é:

i =   - ( h + k ) =   - ( - 1 + 1 ) = 0

Então, o plano é ( 1 _ 101 ) .

Passo 4

Na letra d:

Para esse plano, as interseções com os eixos a 1 ,   a 2   e   z são - a 2 ,   a   e   c 2 , respectivamente. Em termos de a e c, essas interseções são - 1 2 ,   1   e   1 2 , cujos respectivos recíprocos são –2, 1 e 2. Isso significa que:

h =   - 2

k = 1

l = 2

Da Equação 3.7, o valor de i é:

i =   - ( h + k ) =   - ( - 2 + 1 ) = 1

Então, o plano é ( 2 _ 112 ) .

Resposta

  1. (0002)
  2. ( 10 1 _ 0 )
  3. ( 1 _ 101 )
  4. ( 2 _ 112 )
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o fator de empacotamento atômico para o cloreto de césio usando os raios iônicos da Tabela 12.3 e assumindo que os íons tocam-se ao longo das diagonais do cubo.
A partir dos dados na Tabela 12.3, calcule a massa específica teórica do C a F 2 , com estrutura da fluorita.
A célula unitária para o C r 2 O 3 apresenta simetria hexagonal com os seguintes parâmetros da rede cristalina: a = 0.4961 n m e c = 1.360 n m . Se a massa específica desse material é de 5.22 g / c m
O óxido de magnésio tem a estrutura cristalina do sal-gema e uma massa específica de 3.58 g / c m 3 . Determine o comprimento da aresta da célula unitária.Como esse resultado se compara ao comprimento
Calcule a massa específica teórica do diamante dado que a distância C-C e o ângulo de ligação são de 0.154n m e 109.5 º º, respectivamente. Como esse valor se compara à massa específica medida?