No circuito da figura a seguir, encontre as correntes e .
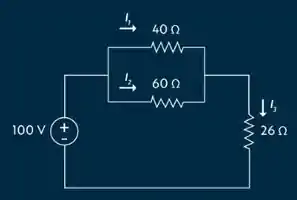
Passo 1
Vamos continuando??
Então galerinha, na primeira parte do caminho a corrente se divide, não é? Isso indica um cicuito em paralelo, depois ela se junta e segue por um único caminho, ou seja, em série!!
Isso nos dá um circuito misto !!
Assustados? Não precisa !! Vamos tirar de letra
Vamos começar calcularndo a resistência equivalente para estes dois resistores em paralelo, lembram da fórmula?
Olhando na figura e substituindo:
Para isolar a resistência equivalente, vamos passar ela para o outro lado da igualdade multiplicando:
E agora o termo do ladinho dela desce dividindo:
E o nosso circuito agora ficará assim:
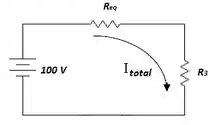
Então, estas duas resistências estão em série e a resistência total é dada por:
Substituindo:
Passo 2
Com a resistência total e a tensão nós conseguimos calcular a corrente pela fórmula:
Para isolar a corrente vamos passa-la para o outro lado multiplicando:
Se queremos a corrente, a resistência tem que passar dividindo:
Substituindo:
Como a corrente total é a corrente que passa no resistor :
Shoow !! Agora só precisamos achar as correntes paras os resistores e !!
E para isso tem uma fórmula bem legalzinha:
Substituindo:
E assim nós chegamos ao fim de mais uma !!