Determine a resistência equivalente do circuito abaixo:
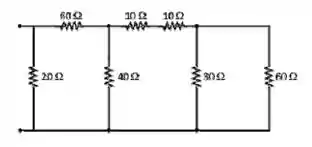
Passo 1
Aaa galerinha, essa daqui é daquelas beem divertidas pra vocês aprenderem a brincar com os circuitos!!
Vamos começar pela combinação mais a direita, ok?
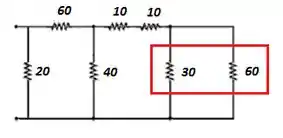
Como a corrente se divide para passar por estes dois caminhos, temos associação em paralelo!! Vamos lembrar da resistência equivalente?
Substituindo:
Para isolar a resistência desconhecida vamos passar ela para o outro lado da igualdade multiplicando:
Agora o termo que acompanha a resistência passa para o outro lado dividindo:
Vamos colocar isso em um desenho:
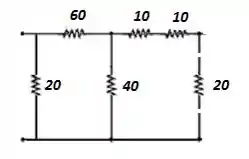
Passo 2
Agora, as resistências e são percorridas por uma única corrente, ou seja, resistores em série:
Substituindo:
E fazendo um desenho:
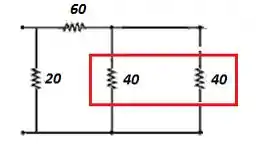
Estes dois resistores são percorridos por duas parcelas da corrente, ou seja, paraleloo!!!
Neste caso:
Como os denominadores são iguais, podemos somar os numeradores:
Dividindo numerador e numerador por 2 para simplificar a fração
Agora vamos multiplicar cruzado:
E o novo desenho:
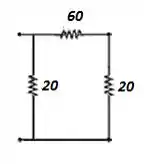
Passo 3
Agora, as resistências 6 e são percorridas por uma única corrente, ou seja, resistores em série:
Substituindo:
E fazendo um desenho:
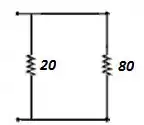
E agora a corrente novamente se divide, certo? E temos uma última associação em paralelo:
Para isolar a resistência desconhecida vamos passar ela para o outro lado da igualdade multiplicando:
Agora o termo que acompanha a resistência passa para o outro lado dividindo:
E assim nós finalizamos mais umaaa!!
Legal, não foi?!