Compense o sistema de retroalimentação unitária com função de transferência mostrada abaixo para melhorar o erro em regime permanente por um fator de 10 vezes para uma entrada degrau, de modo que não altere a resposta transitória do sistema.
Considere que o sistema está operando com polos dominantes em malha fechada em:
Passo 1
O primeiro passo seria fazer a determinação dos polos dominantes em malha fechada. Como o exercício já nos deu de mão beijada essa informação, vamos representar os zeros e polos em malha aberta e os polos dominantes em malha fechada no nosso diagrama.
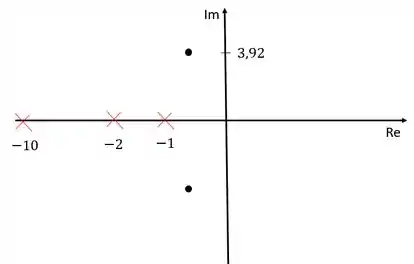
Antes que você me xingue, o desenho não tá feito com a escala certa ok? O importante é só a gente ter uma ideia de como tá o lugar das raízes por enquanto.
Passo 2
O próximo passo é determinar a relação entre o polo e o zero do compensador, já que é isso que fará com que o erro seja reduzido.
Desejamos que o erro seja reduzido dez vezes. Vamos primeiro então calcular o erro sem a presença do compensador
O nosso objetivo adicionando o compensador é que o erro diminua 10 vezes, ou seja, seja de . Para isso:
Passo 3
Agora que já sabemos a relação entre a posição do polo e do zero, já podemos posicioná-los.
Sendo assim, devemos arbitrar um valor para o polo e posicionar o zero seguindo a relação que encontramos.
Lembrando que é preciso que ambos os valores sejam bem baixos. Sendo assim, vamos arbitrar:
Passo 4
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Vamos colocar nossos polos e zeros no diagrama de lugar das raízes para conseguir calcuar o ganho do compensador.
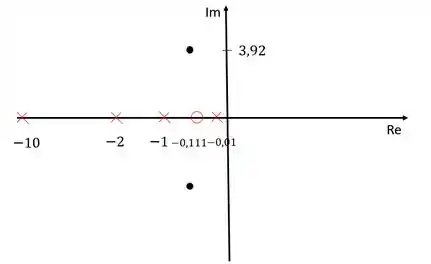
Para calcular o ganho do compensador, devemos usar o critério do módulo, que diz que o produto de todos os módulos é igual a . Sendo que os módulos podem ser calculados como a distância de cada zero/polo ao polo dominante que está repesentado pelo ponto preto.
O polo dominantes, como nós vimos, fica em
Sendo assim, precisamos calcular essas distâncias:
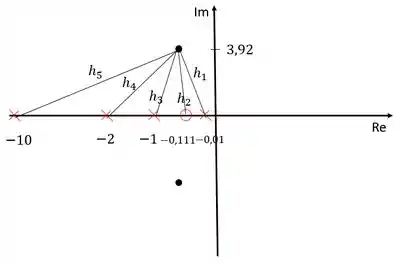
Usando o critério do módulo:
O módulo dos zeros fica no numerador e dos polos no denominador. Precisamos calcular esses módulos agora:
Portanto: