Considere um sistema de retroalimentação unitária com função de transferência mostrada abaixo:
Projete um compensador que resultará em sem alterar significativamente a resposta transitória (overshoot de e tempo se sedimentação para uma faixa de de )
Passo 1
Devemos agora projetar o compensador de atraso de fase que produzirá uma constante, igual a .
O primeiro passo será encontrar o polo dominante em malha fechada. O polo pode ser encontrado através da expressão:
O fator de amortecimento pode ser encontrado diretamente da fórmula do overshoot:
Para um overshoot de :
Para encontrar devemos usar a fórmula do tempo de sedimentação para uma faixa de :
Portanto, o polo dominante será aproximadamente:
Passo 2
Vamos representar no nosso diagrama agora como estamos até aqui.
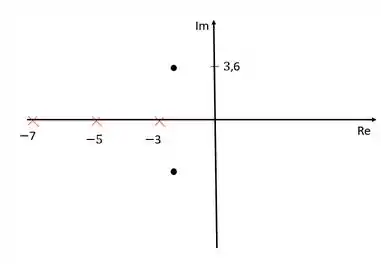
Os “x” vermelhos são os polos em malha aberta da função de transferência, e os pontos pretos são os polos dominantes da resposta.
Passo 3
Precisamos agora implementar nosso compensador. Para isso precisamos encontrar a relação entre as posições do zero e do polo.
Precisamos que o seja iguala a . Com a implementação do compensador, o poderá ser calculado como:
Obs: Para fazer esse cálculo, consideramos o ganho do compensador, , igual a .
Passo 4
Agora que já sabemos a relação entre a posição do polo e do zero, já podemos posicioná-los.
Sendo assim, devemos arbitrar um valor para o polo e posicionar o zero seguindo a relação que encontramos.
Lembre-se que precisamos arbitrar um valor bem pequeno para o polo de modo que o zero e o polo não fiquem muito longe entre si. Uma possibilidade seria:
Passo 5
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Vamos colocar nossos polos e zeros no diagrama de lugar das raízes para conseguir calcuar o ganho do compensador.
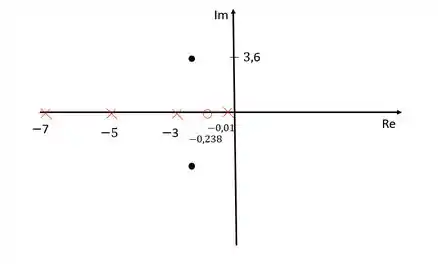
Esse diagrama não está representado com a escala certinha, ok? É só um esboço para a gente ter mais ou menos uma ideia de onde estão as coisas.
Para calcular o ganho do compensador, devemos usar o critério do módulo, que diz que o produto de todos os módulos é igual a . Sendo que os módulos podem ser calculados como a distância de cada zero/polo ao polo dominante que está repesentado pelo ponto preto.
Os polos dominantes, como nós vimos, ficam em
Sendo assim, precisamos calcular essas distâncias:
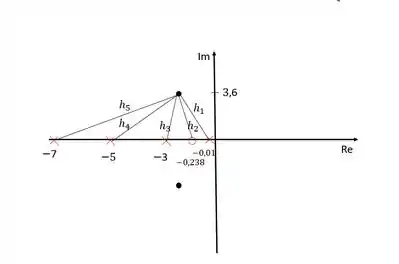
Usando o critério do módulo:
O módulo dos zeros fica no numerador e dos polos no denominador. Precisamos calcular esses módulos agora:
Portanto: