Um sistema com realimentação unitária e função de transferência mostrada abaixo está operando com uma resposta em malha fechada que tem overshoot de e tempo de sedimentação para uma faixa de de
- Qual é o valor da constante de erro estático apropriada?
- Obtenha a função de transferência para uma estrutura de atraso de fase de modo que a constante de erro estático seja igual a 4 sem alterar significativamente os polos dominantes do sistema em compensação.
Passo 1
Para calcular a constante de erro, , devemos fazer o limite na função de transferência já que:
Passo 2
Devemos agora projetar o compensador de atraso de fase que produzirá um igual a .
O primeiro passo será encontrar o polo dominante em malha fechada. O polo pode ser encontrado através da expressão:
O fator de amortecimento pode ser encontrado diretamente da fórmula do overshoot:
Para um overshoot de :
Para encontrar devemos usar a fórmula do tempo de sedimentação para uma faixa de :
Portanto, o polo dominante será:
Passo 3
Vamos representar no nosso diagrama agora como estamos até aqui.
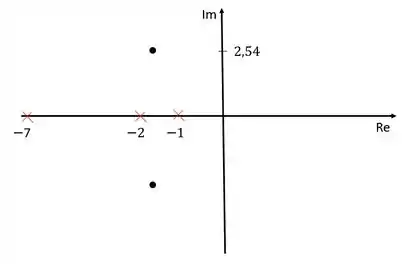
Os “x” vermelhos são os polos em malha aberta da função de transferência, e os pontos pretos são os polos dominantes da resposta.
Passo 4
Precisamos agora implementar nosso compensador. Para isso precisamos encontrar a relação entre as posições do zero e do polo.
Nós queremos que o nosso seja , então:
Passo 5
Agora que já sabemos a relação entre a posição do polo e do zero, já podemos posicioná-los.
Sendo assim, devemos arbitrar um valor para o polo e posicionar o zero seguindo a relação que encontramos.
Lembrando que é preciso que ambos os valores sejam bem baixos.Vamos arbitrar:
Passo 6
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Vamos colocar nossos polos e zeros no diagrama de lugar das raízes para conseguir calcuar o ganho do compensador.
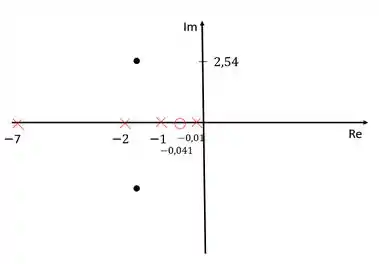
Para calcular o ganho do compensador, devemos usar o critério do módulo, que diz que o produto de todos os módulos é igual a . Sendo que os módulos podem ser calculados como a distância de cada zero/polo ao polo dominante que está repesentado pelo ponto preto.
Os polos dominantes, como nós vimos, ficam em
Sendo assim, precisamos calcular essas distâncias:
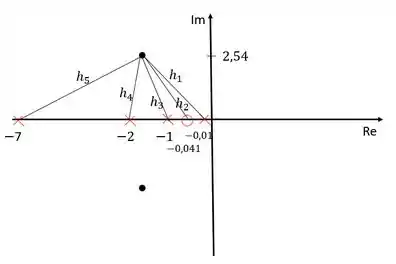
Usando o critério do módulo:
O módulo dos zeros fica no numerador e dos polos no denominador. Precisamos calcular esses módulos agora:
Portanto: