Considere que a placa retangular bidimensional abaixo possua uma condutividade térmica de .
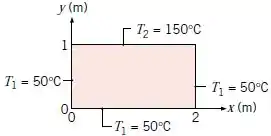
Partindo da solução exata para a distribuição de temperaturas, deduza uma expressão para a taxa de transferência de calor, por unidade de espessura, saindo pela superfície inferior da placa.
Calcule a taxa de transferência de calor considerando os cinco primeiros termos não-nulos da série infinita.
Passo 1
Sabendo que o fluxo térmico muda ao longo de , e que o calor está sendo transferido para fora da placa, o mesmo pode ser calculado da seguinte forma:
Utilizando a relação entre e , temos que:
Assim:
Show de bola! Já sabemos do que precisamos pra chegar à expressão da taxa de transferência de calor.
Passo 2
Sabemos que é dado por:
Pra derivar em relação a , precisamos lembrar que a derivada do é o dessa função. Aí, aplicando a regra da cadeia ali naquele :
Igualando a 0:
Agora podemos seguir com a brincadeira.
Passo 3
Substituindo na expressão da taxa de transferência de calor:
Agora é ir arrumando a bagunça:
Onde e . Assim:
Passo 4
Ok! Queremos trabalhar com os 5 primeiros termos da série, mas repare que, para qualquer valor par de , a série será nula. Assim, vamos considerar os seguintes valores:
Calculando o somatório para cada um dos valores de :
Logo:
![]()