Uma placa retangular bidimensional está sujeita às condições de contorno especificadas.
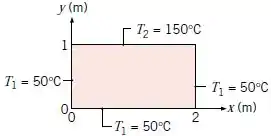
Usando os resultados da solução exata para a equação do calor apresentados na teoria, calcule a temperatura no ponto central , utilizando os cinco primeiros termos não-nulos da série infinita que deve ser determinada.
Passo 1
A distribuição de temperatura é dada por:
Onde e . Como estamos considerando o ponto e , vamos começar substituindo os valores pra ver se conseguimos simplificar a equação:
Passo 2
Para qualquer valor par de , o termo será nulo. Dessa forma, como estamos preocupados em pegar os 5 primeiros termos da série, vamos utilizar os seguintes valores de :
Assim, pegando os 5 primeiros termos da série, teremos:
Jogando isso tudo na calculadora, teremos:
Passo 3
A temperatura central será:
Substituindo os valores:
![]()