Considere o tanque de água que se mostra na figura seguinte:

Para estudar o sistema abriu a torneira e recolheram-se valores da altura da água durante os 10 primeiros minutos, como mostrado na tabela abaixo:
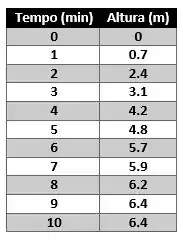
Encontre a curva que melhor se ajusta a esses dados experimentais e preveja o valor da altura após 12 min.
Passo 1
Opa galera, aqui temos uma questão de ajuste experimental que na realidade é apenas um nome bonito que a universidade dá quando quer ajustar um polinômio ou uma função qualquer a um conjunto de números.
Aqui queremos encontrar uma um polinômio que melhor se ajuste aos dados de altura de líquido que foram medidos com o passar do tempo.
Para isso vamos utilizar a função para encontrar o polinômio que melhor se ajuste aos dados experimentais.
Passo 2
Primeiramente para realizar o ajuste precisamos implementar os vetores de dados dentro do Matlab:
![]()
Agora iremos chamar a função polyfit e também vamos inserir uma janela gráfica para verificar se a função realmente está se ajustando bem aos dados.
Sendo assim a função polyfit precisa de três argumentos: o primeiro são os dados da variável ; o segundo são os dados da variável ; e finalizamos inserindo o grau do polinômio para ajustar.
Nós vamos ajustar um polinômio de grau 2, pois ele já demonstra ser um bom ajuste como mostraremos depois.
Sendo assim, temos:
![]()
Para plotar precisamos calcular os valores desse novo polinômio, então vamos criar um vetor auxiliar variando de 0 até 12.
Onde sua utilidade é apenas para usar o com os coeficientes que vamos calcular com a função , gerando as seguintes linhas de código:

E vamos finalizar com a função plot, para podermos visualizar se o ajuste realmente está bom.

Passo 3
Ao executar o código que acabamos de montar geramos o seguinte polinômio:
Onde podemos gerar a seguinte curva:
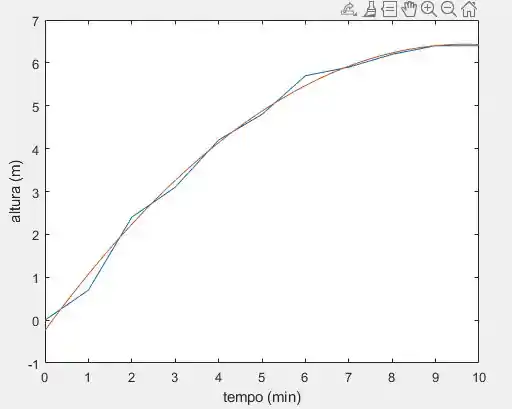
Aqui podemos observar que o ajuste foi consideravelmente bom.
Agora vamos calcular o valor de altura para 12 min, temos que o polinômio nos fornece um valor igual a:

Resposta
O polinômio que teve o melhor ajuste foi um polinômio de grau 2 e o valor da altura em 12 min é uma altura de 6.0509 metros.