O limite de escoamento de muitos metais depende do tamanho das partículas. Para esses metais, a relação entre o limite de escoamento e o diâmetro médio das partículas pode ser modelada pela equação de Hall-Petch conforme mostrado abaixo:
Através de ensaios experimentais foram obtidos os seguintes resultados:

Utilize os dados experimentais e calcule o valor de e de
Passo 1
A questão nos deu dois vetores de dados e pede para encontrarmos o valor das constantes correspondentes na fórmula dada.
Pra resolver, precisamos usar o método de interpolação linear através da função para encontrar o polinômio que melhor se ajusta aos dados experimentais. Uma vez que conseguimos encontrar esse polinômio, por comparação vimos que o coeficiente linear corresponde ao enquanto o coeficiente angular corresponde ao .
Mas você talvez tenha reparado que na tabela temos o diâmetro , enquanto a fórmula tem esse termo dentro de uma raiz . Será que isso dá problema nos nossos cálculos?
Olha só, se em vez de ajustarmos em função de diretamente, nós calcularmos a raiz em cada ponto e ajustarmos em função de , dá tudo certo!
Então é isso que iremos fazer e o algoritmo fica algo mais ou menos assim:
- Entrada de dados (inserir os vetores dado da questão)
- Cálculo do
- Programação do ajuste utilizando a função
- Criação de uma saída de dados para comprar o polinômio com os dados experimentais.
Passo 2
Transformando o algoritmo em programação no Matlab vamos inserir os seguintes pontos:
Primeiramente vamos inserir vetores de dados:

Agora vamos criar o vetor X que é calculado pela seguinte expressão:
Agora vamos inserir a função para o cálculo do polinômio:
Nessa função, os dois primeiros termos dentro dos parênteses representam o conjunto de dados que serão ajustados, no nosso caso em relação a , e por último vem o termo que indica o grau do polinômio que será gerado, no nosso caso .
Passo 3
Uma vez que criamos as funções vamos gerar a saída de dados que corresponde a criação dos seguintes elementos de código:
Como vamos criar um gráfico, vamos criar um vetor no mesmo intervalo dos pontos do eixo com muitos pontos para gerar uma curva contínua:
Agora, precisamos calcular o valor correspondente do polinômio a cada um dos valores de que definimos, pra isso usamos a função .
Nela, o primeiro termo representa os coeficientes do polinômio e são dados pelo que calculamos com a função , enquanto o segundo termo é o valor ou conjunto de valores que vão entrar nesse polinômio, no nosso caso é o vetor que acabamos de definir:
Agora vamos criar dois plot juntos, o primeiro com os valores de e que usamos para encontrar o polinômio e o segundo com os valores de e que representam a reta que encontramos através da interpolação linear:
O código completo em Matlab deve ficar algo mais ou menos assim:

E gerando o seguinte gráfico:
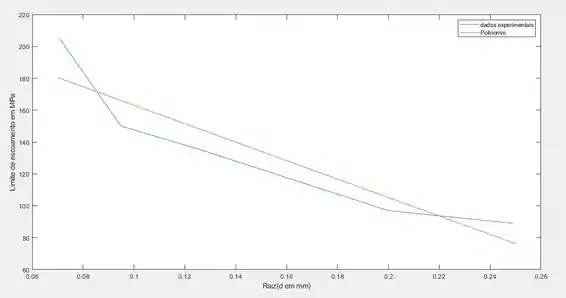
Cujo os coeficientes são dados pelos seguintes valores:
![]()
Resposta
Analisando os coeficientes obitidos pelo ajuste dos dados experimentais podemos concluir que: