A equação de estado do gás ideal ela relaciona volume, pressão, temperatura e quantidade molar através da seguinte expressão:
Onde R, V, P e T são respectivamente a constante universal dos gases, volume, pressão e temperatura do gás.
Em um experimento um aluno de engenharia confinou em um reservatório 0.05 mol de gás em um recipiente, ao aquecer o gás observou a variação da pressão e do volume conforme a temperatura aumentava, gerando os seguintes dados:

Utilize os dados fornecidos para ajustar um polinômio de primeiro grau de V em função de
E assim caracterize o valor da constante universal dos gases e compare com os valores da literatura para justificar se o ajuste foi válido.
Passo 1
A questão é uma aplicação quase direta do segundo método para criação de polinômios, ele deu três vetores de dados e pede para encontrar o polinômio que melhor se ajuste aos dados experimentais.
Mas antes de irmos para o código precisamos primeiramente regredir de 3 vetores para 2, para assim poder fazer o ajuste linear, então o algoritmo fica:
- Entrada de dados ( inserir os vetores dado da questão)
- Cálculo do
- Programação do ajuste utilizando a função
- Criação de uma saída de dados para comprar o polinômio com os dados experimentais.
Passo 2
Transformando o algoritmo em programação no Matlab vamos inserir os seguintes pontos:
Primeiramente vamos inserir vetores de dados e colocando a temperatura em kelvin:

Agora vamos criar o vetor X, lembrando que vamos dividir elemento a elemento:
Agora vamos inserir a função para o cálculo do polinômio:
Uma vez que criamos as funções vamos gerar a saída de dados que corresponde a criação dos seguintes elementos de código:
Criação de um vetor para a variação contínua da curva e a criação da própria curva:
Agora vamos criar o plot:
O código em Matlab deve ficar algo mais ou menos assim:

Executando podemos obter os seguintes resultados:
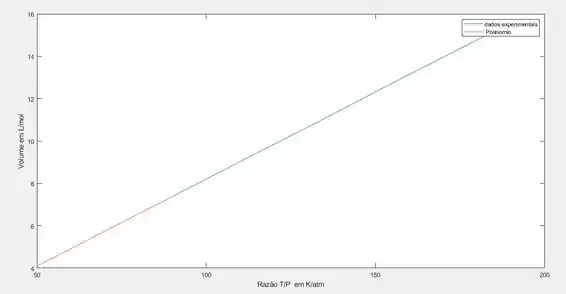
Cujo os coeficientes são dados pelos seguintes valores:
![]()
Resposta
Encontramos com o ajuste um valor de e a literatura(google) informa:

Então o nosso ajuste conseguiu prever com eficiência o valor da constante universal dos gases.