Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Deformações em estruturas com inércia variando aleatoriamente (Regra de Simpson)

Ver Teoria
Exercício 61234578

Enunciado

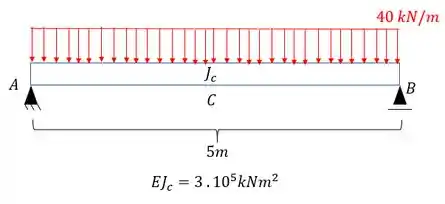
Para a viga abaixo com inércia constante, determine o deslocamento vertical do ponto C usando a regra de Simpson;

Passo 1

A primeira coisa que devemos notar é que nossa estrutura é uma estrutura isostática, logo, não precisaremos quebrar nenhum vínculo para determinação de hiperestáticos:

A segunda coisa que devemos fazer é dividir a nossa seção em uma quantidade par de seções, pois lembre-se que para usarmos essa fórmula:

E J c δ = ∆ x 3   4 ∑ η í m p a r e s + 2 ∑ η p a r e s + 1 ∑ η d a s   e x t r e m i d a d e s

Precisamos de uma quantidade par de seções, e que podemos determinar os coeficientes das seções seguindo a seguinte regra:

Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente k = 4 . Todas as seções pares com k = 2 e todas as extremas com k = 1 .

Sendo assim, como a inércia é constante, vamos dividir em 10 seções afim de ficarmos o mais próximo possível do valor real, teremos assim que:

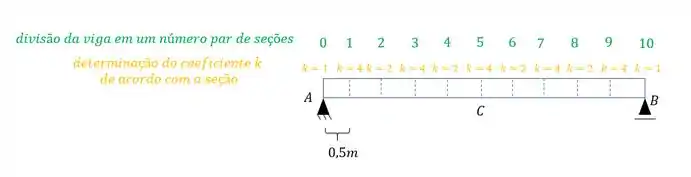
Também definimos no nosso exemplo que o valor de ∆ x é de 0,5m, além do mais dividimos a nossa estrutura em 10 seções (um número par de seções) com tamanhos iguais.

Agora só falta determinarmos o valor de: η í m p a r e s , η p a r e s e η d a s   e x t r e m i d a d e s .

Sabemos que η nada mais é que uma simplificação da seguinte conta:

M M ¯ J c J

Em que:

M = m o m e n t o s   f l e t o r e s   e m   c a d a   s e ç ã o   n o   s i s t e m a   c o m   a   c a r g a   r e a l  

M ¯ = m o m e n t o   e m   c a d a   s e ç ã o   d e v i d o   a   c a r g a   u n i t á r i a

J = m o m e n t o   d e   i n é r c i a   d a   s e ç ã o   a n a l i s a d a  

J c = m o m e n t o   d e   i n é r c i a   d e   r e f e r e n c i a ,   q u e   g e r a l m e n t e   u s a m o s   a   s e ç ã o   c o m   m e n o r   a l t u r a  

Passo 2

No nosso exemplo isostático queremos saber o deslocamento vertical do ponto C, sendo assim podemos dizer que:

  • Diagrama de momentos fletores para o carregamento externo para cada uma das seções será

  • Diagrama de momentos fletores devido a carga unitária no ponto e na direção que queremos saber o deslocamento, que nesse caso é deslocamento vertical:

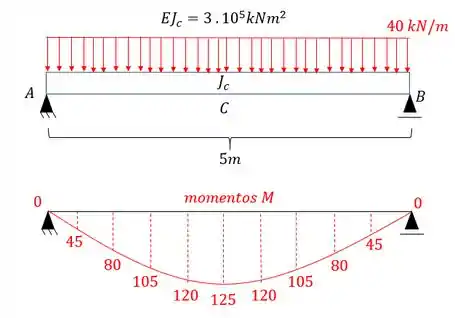
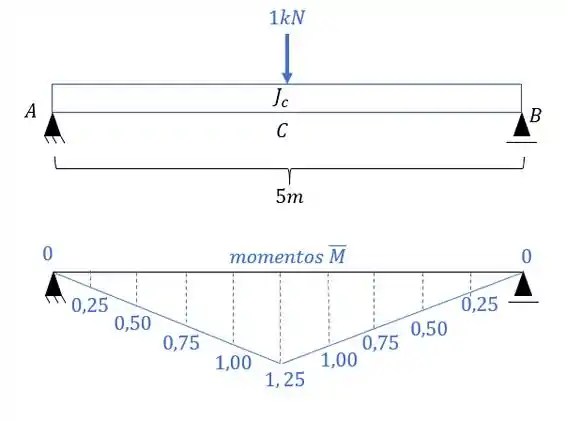
E agora por fim só precisamos relacionar os J e J c .

no nosso caso a seção é constante, ou seja, a relação entre J será constante e igual a 1, sendo assim teremos que se substituirmos na fórmula teremos que:

M M ¯ J c J = M M ¯

Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente.

No fim basta fazer:

E J c δ = ∆ x 3 ∑ K η

E assim determinar as deformações no nosso sistema. No nosso exemplo teremos que:

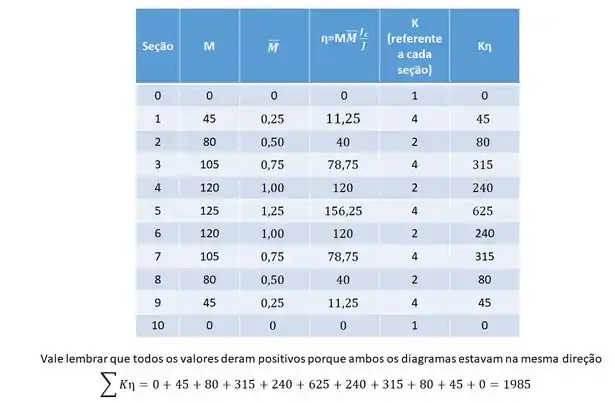
Substituindo na fórmula teremos que:

E J c δ = ∆ x 3 ∑ K η

E J c = 3   .   10 5 k N m 2

∑ K η = 1985

∆ x = 0,5

3   .   10 5 .   δ = 0,5 3 . 1985

δ = 0,001103   m

δ = 1,103   m m

Resposta

δ = 1,103   m m