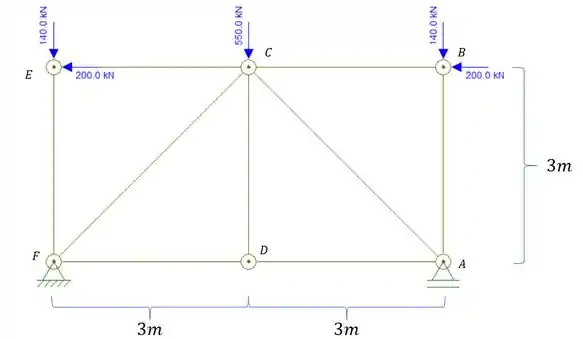
Calcule o deslocamento vertical do ponto C, para a treliça abaixo. Usar para todas as barras da treliça:
Passo 1
Como queremos saber o deslocamento da nossa estrutura já sabemos que antemão que podemos usar a seguinte fórmula
Sabemos também que em treliças podemos desprezar três parcelas (devido ao momento, ao cortante e ao torque). Com isso nossa fórmula passa a ser.
Como temos várias barras, iremos precisar calcular o diagrama de todas elas, logo teremos
E como todas as barras possuem o mesmo módulo de elasticidade e a mesma área, a nossa fórmula fica sendo, de maneira simplificada o seguinte.
Em que precisamos determinar os diagramas normais tanto para o caso unitário quanto para o caso real.
Passo 2
Como queremos determinar o deslocamento vertical na direção vertical, basta aplicarmos uma carga unitária no ponto em que se deseja determinar o deslocamento, e na direção desejada, nesse caso, uma vertical em C.
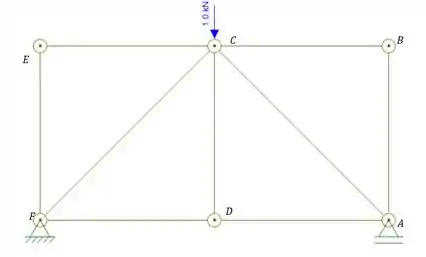
Fazendo o diagrama de corpo livre temos que a reação de apoio será dada por
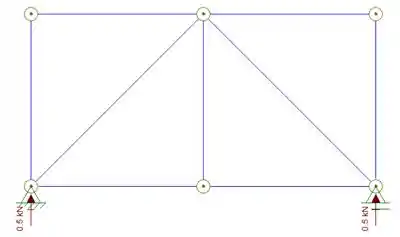
Tendo as reações de apoio traçamos o diagrama de normais da treliça devido a carga unitária (não iremos detalhar essa parte nessa aula, mas falamos muito sobre isso no tópico solução de treliças no assunto Treliças e estruturas isostáticas)
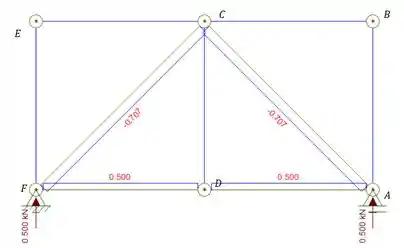
Perceba que alguns normais são iguais a zeros, o que podemos usar para simplificar a nossa equação, sabemos que:
Logo a nossa equação será
E lembre-se que no caso de treliças as equações dos normais serão constantes, que serão escritos como:
Passo 3
Agora precisamos fazer o mesmo diagrama para a estrutura real do nosso problema. Nossa estrutura real é:
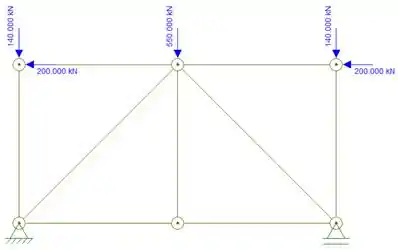
Calculando as reações de apoios teremos que:
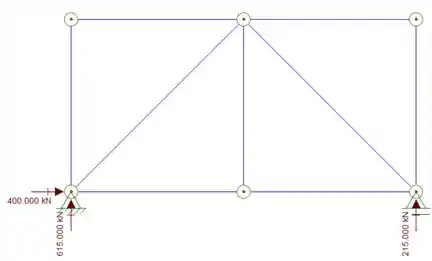
Com as reações de apoio podemos determinar os diagramas de normais
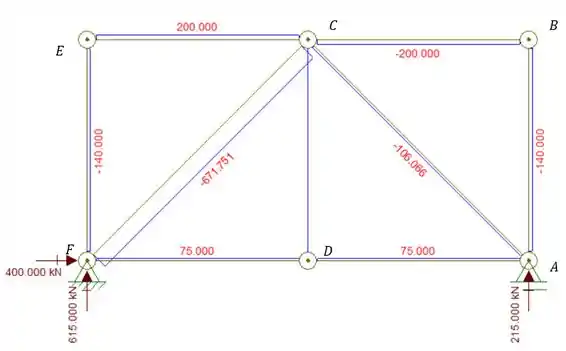
Perceba que com a nossa equação simplificada só iremos precisar do valor de 4 barras, que são:
Passo 4
Precisamos determinar o comprimento de cada uma das barrinhas da nossa treliça, para podermos substituir tudo na nossa fórmula. Fazendo Pitágoras vamos encontrar que:
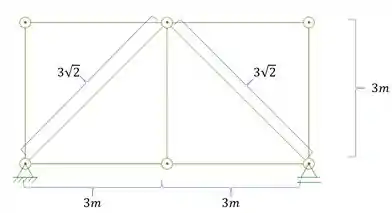
Passo 5
Agora basta juntarmos na nossa fórmula cada uma das equações encontradas
perceba que o deslocamento deu positivo, ou seja, arbitramos a carga unitária na direção correta do que de fato a estrutura se movimenta, e por isso tivemos um valor positivo.