Determine o deslocamento horizontal do ponto . Utilizar
Passo 1
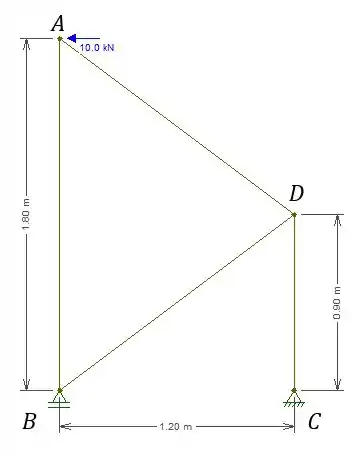
Fala aí, pessoal!!! Olha só para começar esse exercício a gente precisa entender que o ponto é um apoio com liberdade para deslizar horizontalmente e o problema quer exatamente isso, o deslocamento horizontal de !!
Para resolver isso vamos utilizar aquela nossa equaçãozinha de trabalho virtual:
Mas a gente tem que lembrar também que para treliças a gente pode desprezar as parcelas: do momento, do cortanto e do torque; e obter:
Passo 2
Para resolver a equação acima a gente precisa dividir ela em cada seção da treliça, dessa forma vamos ter:
Vale lembrar que o termo é constante e igual para todos, logo:
Agora a gente vai precisar achar as normais virtuais e as normais reais para cada barra (você pode chamar de normais normais que fica mais legal também uahsuashuashusa)
Passo 3
Para achar as normais virtuais a gente vai aplicar uma força horizontal unitária em da seguinte forma:
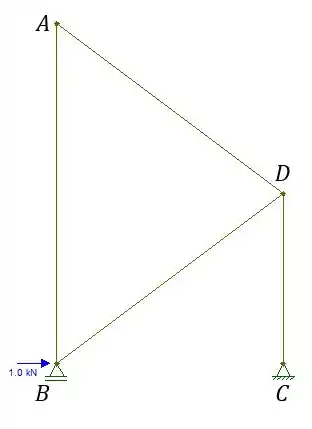
Aplicamos em porque queremos o deslocamento em . É horizontal porque queremos o deslocamento horizontal. É unitária porque é SEMPRE unitária!
Pessoal, como o foco desse conteúdo não é ficar calculando reações e normais eu vou mostrar direto aqui quais serão esses valores:
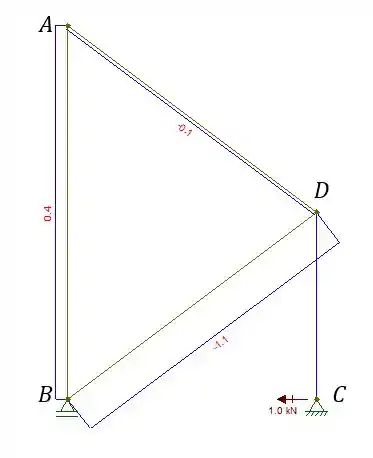
Então vamos ter o seguinte:
Passo 4
Agora vamos achar as normais reais, vamos fazer isso utilizando o carregamento fornecido:
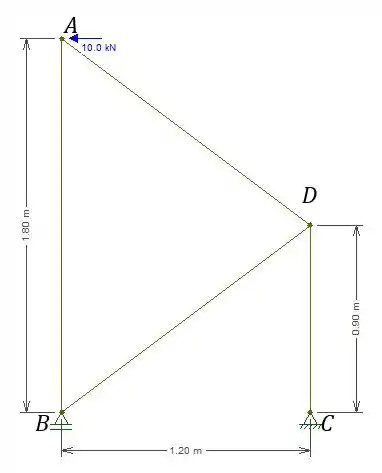
Novamente eu vou mostrar a vocês o resultado final, lembrando que o foco desse tópico não é ficar calculando essas reações e normais:
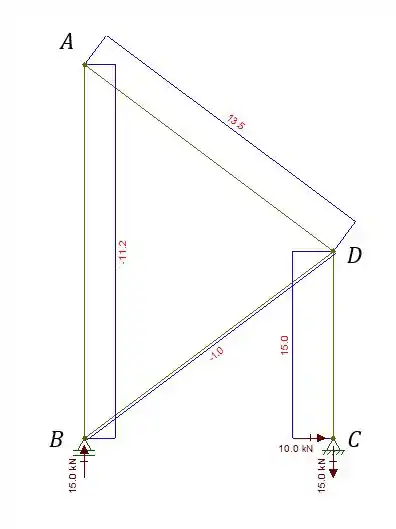
Então vamos ter o seguinte:
Passo 5
Agora a gente tem que achar os comprimentos de cada barra:
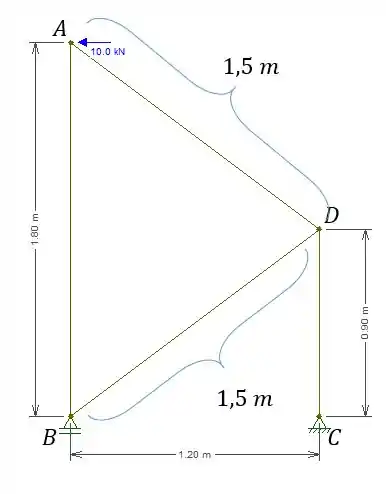
Passo 6
Agora é só substituir na equação:
Lembrando que o termo