Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Deslocamento em estruturas isostáticas- Temperatura e Recalque.

Ver Teoria
Exercício 51234678

Enunciado

Um pórtico possui as fibras da parte superior com uma temperatura de 60°C e da parte inferior com 20°c. sabendo disso determine o deslocamento vertical o ponto B. Use: Seção da viga 30   c m de alma por 90 cm de altura (viga retangular) e α = 1.10 - 5 ° C - 1

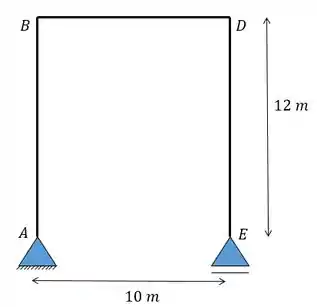
Passo 1

Sabemos que para cálculo da temperatura usamos a seguinte equação:

P ¯ δ = ∫ N ¯ α t g d s + ∫ M ¯ α ∆ t h d s

Como trata-se de barras iguais vamos poder simplificar da seguinte forma:

P ¯ δ = α t g ∑ A N ¯ + α ∆ t h ∑ A M ¯

Além disso, para esse caso não haverá momento fletor, logo podemos simplificar ainda mais:

P ¯ δ = α t g ∑ A N ¯

Então a gente precisa basicamente achar os diagramas da normal para resolver essa questão.

Passo 2

Aplicando a força unitária vertical em B vamos ter:

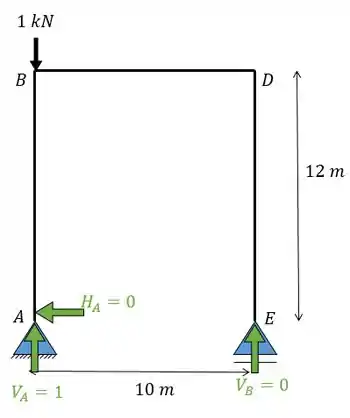
Desenhando o diagrama da normal para cada barra vamos ter:

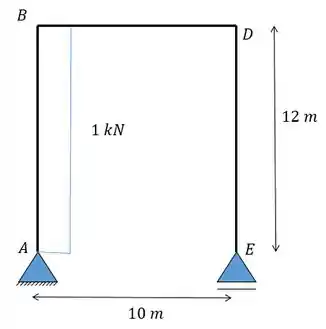
Agora podemos calcular a área do diagrama lembrando que trata-se de uma compressão logo o termo será negativo:

∑ A N ¯ = - 1 × 12 = - 12

Passo 3

Agora é substituir os termos na nossa fórmula. Aqui vale lembrar que temos uma seção retangular então o centroide da seção coincide com a temperatura média.

P ¯ δ = α t g ∑ A N i

P ¯ = 1   k N

α = 1.10 - 5 ° C - 1

t g = 60 + 40 2 = 50 ° C

∑ A N i = - 12

Substituindo teremos que:

P ¯ δ = α t g ∑ A N i

1 . δ = 1.10 - 5 . 50 . ( - 12 )

δ = - 0,006   m

Como o deslocamento deu negativo ele se dá no sentido inverso da carga unitária. Ou seja, o deslocamento será para cima.

Resposta

O deslocamento tem valor de 6   m m para cima.