Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Deslocamento em estruturas isostáticas- Temperatura e Recalque.

Ver Teoria
Exercício 41235678

Enunciado

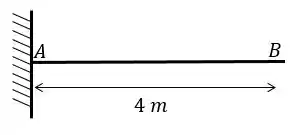
Uma viga possui as fibras da parte superior com uma temperatura de 25 °C e da parte inferior com 45 °C. sabendo disso determine o deslocamento vertical do ponto B. use:

E J = 15   .   10 5

s e ç ã o   d a   v i g a = 20   c m   d e   a l m a   p o r   60   c m   d e   a l t u r a   ( v i g a   r e t a n g u l a r )

α = 1.10 - 1 ° C - 1

Passo 1

Fala, pessoal!!! Tudo tranquilinho com vocês? Galera, tá na cara que essa questão é uma questão de deslocamento devido à temperatura não tá não? Então para resolvermos esse problema usamos a seguinte equação:

P ¯ δ = ∫ N ¯ α t g d s + ∫ M ¯ α ∆ t h d s

Lembrando que o problema quer o deslocamento vertical do ponto B .

Como só existe uma barra de seção constante a gente pode utilizar a seguinte simplificação.

P ¯ δ = α t g ∑ A N ¯ + α ∆ t h ∑ A M ¯

Além disso não existem a componente da normal então vamos ter:

P ¯ δ = α ∆ t h ∑ A M ¯

Passo 2

Então vamos achar o diagrama de momento fletor devido à carga unitária. Lembrando que essa carga unitária deve ser posicionada no ponto em que queremos saber o deslocamento B e na direção em que queremos saber o deslocamento (vertical). Dessa maneira teremos que:

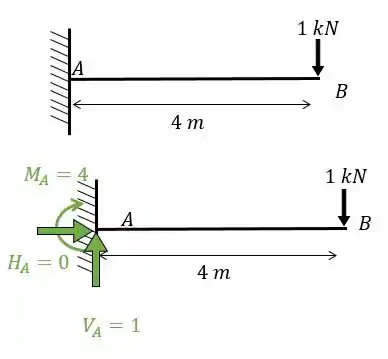
Desenhando o diagrama teremos que:

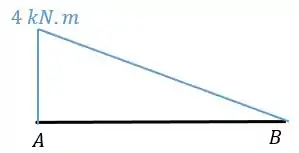
E a área é dada por

A M - = 1 2 × 8 × 4 = 16

Passo 3

Agora é substituir os termos na nossa fórmula

P ¯ δ = α ∆ t h ∫ M ¯ d s

P ¯ = 1   k N

α = 1   .   10 - 5   ° C - 1

h = 0,6   m

∆ t = t i - t s = 45 ° - 25 ° = 20 ° C

A M - = 16   k N . m

Substituindo teremos que:

P ¯ δ = α ∆ t h ∑ A M ¯

1 . δ = 1.10 - 5 . 20 0,6 × 16

δ = 5,33.10 - 3   m

δ = 5,33   m m

Resposta

δ = 5,33   m m