Supondo que o apoio A sofreu um deslocamento vertical para cima de , e o apoio B sofreu um deslocamento vertical para baixo de . Determine o deslocamento vertical do ponto C do pórtico.
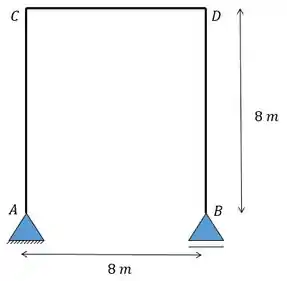
Passo 1
Fala aí, galerinha!!! Esse problema trata sobre recalques, recalque é outra forma de dizer que houve um deslocamento, beleza?
Depois que esses deslocamentos descritos no enunciado aconteceram o nosso pórtico vai mudar e outros pontos também irão se deslocar, correto? O problema quer saber qual será o deslocamento final do ponto .
Para isso vamos utilizar nossa equaçãozinha de recalque:
Nós vamos debater sobre como utilizar essa equação conforme formos resolvendo o exercício, de qualquer forma o importante agora é lembrar que:
- Devemos aplicar uma carga unitária em .
- Calcular as reações dos apoios devido à carga unitária.
- Analisar os deslocamentos dados.
- Colocar tudo isso dentro da equação
Passo 2
A primeira coisa que devemos fazer é pôr uma carga unitária no ponto em que se deseja saber o deslocamento e na direção que se deseja conhecer o deslocamento. No nosso caso é no ponto C e vertical para baixo. Vamos aproveitar e representar as forças de reação nos apoios também.
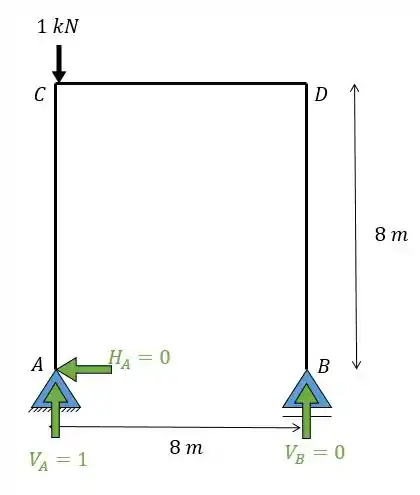
Passo 3
Agora nós vamos analisar os deslocamentos dados. Isso consiste em colocar no nosso pórtico os deslocamentos fornecidos no problema ().
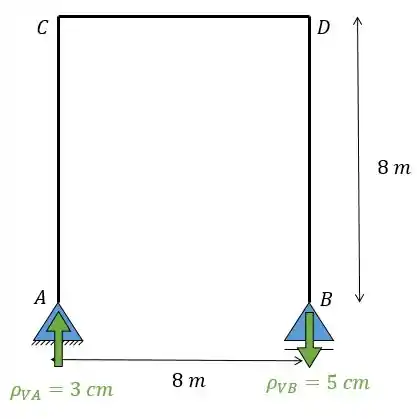
Passo 4
Agora precisamos ficar bem atentos, a nossa fórmula é
Aqui precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
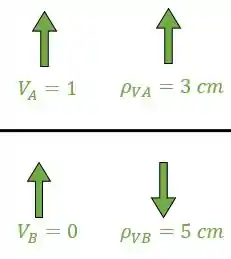
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
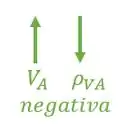
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,

e sempre que for no sentido contrário, será negativa.
Passo 5
Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Substituindo os valores e lembrando que nossa carga unitária vale
O sinal negativo significa que o deslocamento se dá no sentido inverso da força unitária aplicada. Como colocamos a força para baixo o deslocamento do ponto C não se dá para baixo, mas sim, para cima.