Calcule os parâmetros do modelo log-normal para a seguinte amostra:
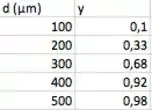
Passo 1
Temos uma tabela com pares (), com diâmetros em e temos que calcular os parâmetros do modelo log-normal. A grande questão desse exercício é que o modelo log-normal NÃO é linearizável. Portanto, vamos ter que resolver graficamente.
Vamos começar plotando, num gráfico, . Vou fazer no excel, mas se fosse em uma prova, você provavelmente teria papel milimetrado.
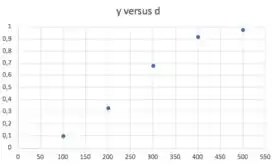
Vamos precisar, também, traçar um esboço do formato da curva , passando por esses pontos. No papel milimetrado, você faria à mão livre mesmo. Como estou no excel, vou pedir pra ele um gráfico com linhas suaves:
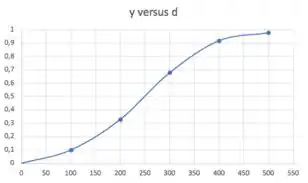
Passo 2
A expressão para , isto é, em função do diâmetro, segundo o modelo log-normal, é:
Seus parâmetros são e . Lembrando, da teoria, como calcular cada um deles:
Então, temos que ir no gráfico e pegar pontos. Bora começar com o . Daí, precisamos achar o diâmetro que faz .
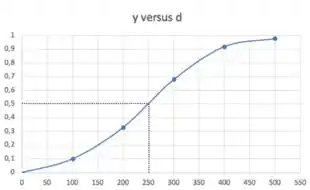
Eu coloquei “aproximadamente” porque estamos trabalhando com método gráfico, daí, estamos obtendo estimativas né.
Agora, falta calcular o . Para isso, precisamos ou do ou do . Vou pegar o .
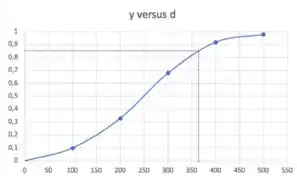
E bota aproximado nisso! Mas estamos no método gráfico então há limitações né.
Calculando :