A peneiração de uma amostra de areia gerou a seguinte distribuição de tamanhos:

Pede-se:
- Dentre os modelos GGS, sigmóide e RRB, indicar qual melhor descreve a referida análise.
Passo 1
Nessa questão, ele deu pares () e pede qual o melhor modelo dentre o GGS, sigmóide e RRB. Vamos ter que avaliar o coeficiente de correlação depois de linearizar e jogar na calculadora: quanto mais próximo de o coeficiente de correlação for, significa que melhor o tal modelo representa a amostra.
Vou trabalhar com o (se você preferir, pode usar o r; a ideia é a mesma).
Primeiro de tudo, temos que usar o em base unitária em todas as contas, então, vou adicionar uma linha nessa tabela aí logo:

E, como eu te disse lá na teoria, vamos desprezar, para linearizações, pontos com e pontos com . Daí, vou cortar logo esse último ponto aí:

Bora ver agora um por um:
Passo 2
Primeiro, bora ver o GGS. A fórmula pra no GGS é:
Linearizando, fica:
Daí, vamos ter que montar uma tabelinha com e :

Como vimos na teoria, comparando essa nossa equação linearizada com a equação de uma reta, :
Daí, vamos fazer uma regressão linear com os pontos ( , ):
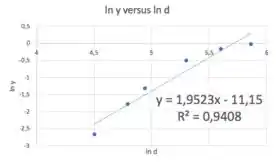
Para avaliar qual o melhor modelo pra representar uma amostra, só precisamos dessa informação aí de . Então guarda aí:
Passo 3
Vamos ver, agora, o Sigmóide. A fórmula dele pra é:
Linearizando:
Comparando com a equação de uma reta:
Montando nossa tabelinha com e :
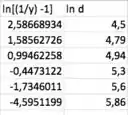
Fazendo a regressão linear:
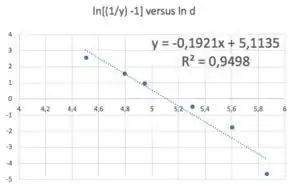
Guarda aí, também:
Passo 4
Falta só o RRB agora. Bora lá! A fórmula de para o RRB é:
Linearizando:
Comparando com a equação de uma reta:
Fazendo a tabelinha com e :
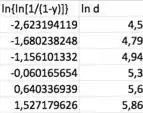
Fazendo a regressão linear:
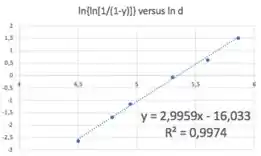
Guarda aí:
Passo 5
O mais trabalhoso já foi. Agora é só comparar os dos 3 modelos.
Como é o maior dentre os , isto é, o mais próximo de , o RRB é o melhor modelo pra representar ESSA AMOSTRA.
Resposta
RRB, pois o da sua linearização é o mais próximo de 1, ou seja, o maior dentre os modelos analisados.