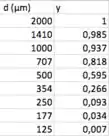
Estimar os parâmetros do modelo de Weibull para a seguinte amostra:
Passo 1
Nessa questão, temos uma tabela com pares (), com o diâmetro em , e é pedido para estimar os parâmetros do modelo Weibull para essa amostra. Bora lembrar da equação de para esse modelo:
Os parâmetros dele são: e . Ou seja, 3 parâmetros para determinar.
Como vimos na teoria, uma reta tem 2 parâmetros então não dá pra linearizar o Weibull assim, com esses 3 parâmetros desconhecido. Mas se tivermos como determinar algum deles, conseguimos linearizar, já que só vão sobrar 2 parâmetros.
Passo 2
A primeira coisa pra fazer é determinar o , que é o parâmetro que temos como estimar graficamente. Dessa forma, vão sobrar 2 parâmetros a determinar e aí conseguimos linearizar e fazer regressão linear para calcular e . Bora lançar esses pares () num gráfico:
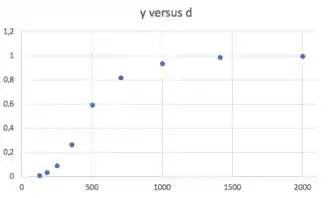
Numa prova, você faria lançaria esses pontos num papel milimetrado.
Depois, o que temos que fazer é traçar a mão a curva , passando por esses pontos. Daí, vemos a interseção da curva com o eixo , que é o eixo do diâmetro, e esse será o , isto é, o parâmetro . Vou fazer isso agora, dando um zoom nos pontos mais próximos desse pra facilitar da gente enxergar o :
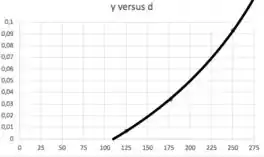
Daí:
Passo 3
Agora que temos o , só restam 2 parâmetros a determinar e aí conseguimos linearizar e fazer regressão linear. Como vimos na teoria, a forma linearizada da equação de Weibull, conhecido o , é:
Comparando com a equação de uma reta, :
Daí, precisamos de uma tabela com os pares (), isto é, pares ( ), lembrando que, na hora de linearizar, desprezamos pontos com e/ou .
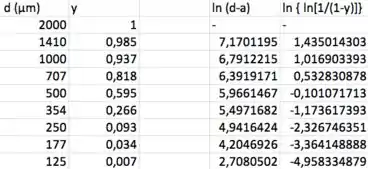
Fazendo a regressão linear:
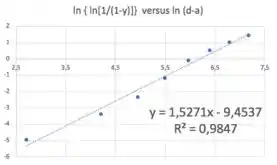
Daí:
E
Substituindo o valor de nessa ultima equação:
Cortando os menos e isolando :
E como os diâmetros estão em :