A partir de uma curva de erro gaussiana, qual a probabilidade de um resultado de
uma população estar contido entre e em relação à média? Qual a probabilidade
de o resultado ocorrer entre e em relação à média?
Passo 1
Vamos começar dando uma olhadinha na curva de erro gaussiana!!
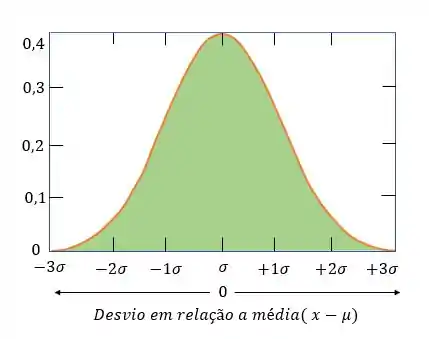
Sabendo que dos dados estão entre , entre e entre ! Se dos dados estão em torno de então a probabilidade do resultado esta entre e é a metade deste:
Passo 2
Agora a gente pode dividir as regiões da curva:
Logo da curva esta dividido entre e e e , para achar a probabilidade de um resultado de uma população estar contido entre e dividimos esse valor por :
Para vizualizamos melhor a curva segue a seguinte distribuição:

Aweee!!