Correção do Fator de Potência
Produzido por Alexandre NunesTeoria
A maioria dos eletrodomésticos utilizados na nossa casa (como máquina de lavar roupa, ar-condicionado e refrigeradores) e a maioria dos motores nas indústrias, são cargas indutivas e operam com um fator de potência baixo e com atraso. Por conta disso, é necessário fazer a correção do fator de potência.
Procedimento de correção
O processo de aumentar o fator de potência sem alterar a tensão ou corrente para a carga original é conhecido com correção do fator de potência. E como a gente faz isso? Colocando um capacitor em paralelo com a carga indutiva.
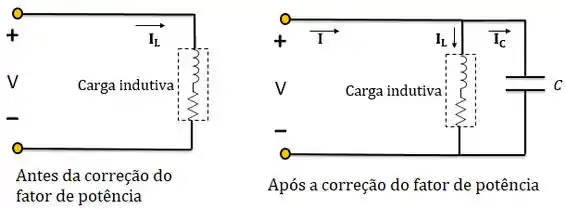
Uma das coisas em que estaremos interessados, será calcular o valor do capacitor inserido em paralelo para corrigir o fator de potência. Lembrando que:
De acordo com a Lei de Ohm:
Além disso:
Substituindo em
Finalmente, substituindo na equação deduzida acima:
O valor de é dado pela variação de potência reativa quando há a correção do fator de potência. Ou seja, diminuímos a potência reativa. Logo:
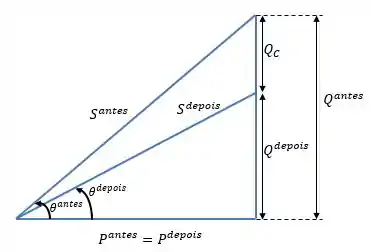
Vamos resolver um exemplo para você entender melhor.
Supondo que haja uma carga conectada à rede elétrica de , Hz, que absorva da rede com um fator de potência atrasado de. Determinar o valor da capacitância necessária para elevar o fator de potência para .
Passo 1:
Como foi dito no enunciado, o fator de potência é atrasado. Isso significa que a carga é predominantemente indutiva e, portanto, teremos que corrigir o fator de potência.
Identificando os dados do enunciado:
Passo 2:
O ângulo do fator de potência antes da correção é:
Agora, precisamos calcular a potência reativa antes da correção do fator de potência. Para isso, temos que calcular a potência aparente:
Logo:
Passo 3:
O ângulo do fator de potência depois da correção será:
Quando colocamos o capacitor para corrigir o fator de potência, a potência ativa não muda. Então, para calcular a potência aparente depois da correção do FP, utilizaremos a mesma potência ativa:
Logo, a potência reativa será:
Passo 4:
Agora já temos todos os dados para calcular o valor do capacitor. Falta só calcular o valor de .
Logo, vamos calcular o valor do capacitor:
Agora é fazer bastante exercício!
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.438, Problema 11.39
Um motor CA com impedância Ω é alimentado por uma fonte de 220V e 60Hz.
- Determine o FP, P e Q.
- Determine o capacitor necessário para ser conectado em paralelo com o motor de modo que o fator de potência seja corrigido para a unidade.
Passo 1
Vamos começar pelo fator de potência, já que foi fornecido o valor da impedância do circuito. Lembrando que o fator de potência é o cosseno do ângulo da impedância. Então, passando a impedância para a forma polar:
Passo 2
O circuito do problema é este:
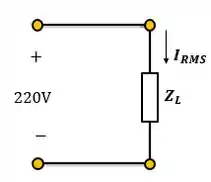
Precisamos, então, calcular a corrente do circuito. Então, de acordo com a Lei de Ohm:
Passo 3
Agora já podemos calcular a potência ativa:
Passo 4
Calculando a potência reativa:
Passo 5
Precisamos, agora, calcular o valor do capacitor que corrige o fator de potência para o valor unitário. Ou seja:
Ou seja: pede-se que o ângulo do fator de potência após a correção seja . Isso quer dizer que:
Sendo que:
Logo:
Passo 6
A fórmula para o cálculo do capacitor para correção do FP é essa:
Logo, falta calcularmos :
Passo 7
Finalmente:
Resposta
Exercício Resolvido #2
Livro Sadiku, p.441, Problema 11.74
Uma fonte de , alimenta duas cargas conectadas em paralelo, como mostra a figura abaixo.
Determine o fator de potência da associação em paralelo. Calcule o valor da capacitância conectada em paralelo que elevará o fator de potência para um valor unitário.
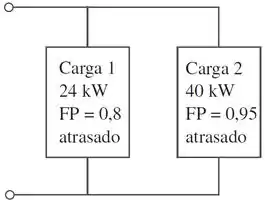
Passo 1
Para determinar o fator de potência da associação em paralelo vamos calcular a potência complexa de cada carga e depois somá-las.
O ângulo da potência complexa total será o ângulo do fator de potência. Para isso, vamos usar muito o triângulo das potências.
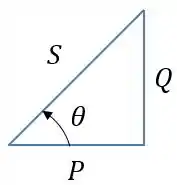
Passo 2
Primeiro, vamos calcular a potência complexa relacionada a carga 1. Sobre essa carga, sabemos:
Como o fator de potência é atrasado, o ângulo é positivo e será:
Utilizando o triângulo das potências, temos:
Então, a potência aparente da primeira carga será:
Agora que encontramos a potência aparente e o ângulo do fator de potência, já podemos determinar a potência complexa da primeira carga:
Passando para forma retângular:
Passo 3
Agora vamos calcular a potência complexa relacionada a carga 2. Sobre essa carga, sabemos:
Como o fator de potência é atrasado, o ângulo é positivo e será:
Utilizando o triângulo das potências, temos:
Então, a potência aparente da segunda carga será:
Agora que encontramos a potência aparente e o ângulo do fator de potência, já podemos determinar a potência complexa da segunda carga:
Passando para forma retangular:
Passo 4
Agora vamos somá-las:
Agora vamos passar para a formula polar, já que o ângulo da potência complexa é igual ao ângulo do fator de potência.
Portanto, o fator de potência será:
Passo 5
Precisamos, agora, calcular o valor do capacitor que corrige o fator de potência para o valor unitário. Ou seja:
Ou seja: pede-se que o ângulo do fator de potência após a correção seja . Isso quer dizer que:
Sendo que:
Logo:
Além disso, como , antes da correção a potência reativa é:
Passo 6
A fórmula para o cálculo do capacitor para correção do FP é essa:
Logo, falta calcularmos , que corresponde a parcela da potência reativa referente ao banco de capacitores que estamos instalando no circuito.
Passo 7
Finalmente:
Resposta
Exercício Resolvido #3
Livro Sadiku, Problema 11.39
Um motor CA com impedância é alimentado por uma fonte de
(a) Determine FP, P e Q.
(b) Determine o capacitor necessário para ser conectado em paralelo com o motor de modo que o fator de potência seja corrigido para a unidade.
Passo 1
Para calcular o FP, vamos primeiro passar a impedância para a forma polar para facilitar as contas:
Então, o Fator de Potência será:
Passo 2
Agora, para calcular as potências ativa (P) e reativa (Q), vamos primeiro achar a potência aparente (S):
, onde Z* é o conjugado, ou seja, basta trocar o sinal do ângulo (ou da parte imaginária)
Passando a potência aparente para a forma retangular, teremos
Sabemos que a Potência Ativa é a parte real e a Potência Reativa é a parte imaginária, então basta separar.
Passo 3
Para corrigir o Fator de Potência para FP =1, ou seja, Potência Reativa nula, vamos adicionar um banco de capacitores e é isso que queremos dimensionar; qual o tamanho do capacitor?
É assim:
, onde é a corrente do capacitor que é
E
Juntando as três, chegamos em , onde
Mas… quem é ?
Então,
Então, como
Resposta
(a)
(b)