Potência Complexa
Produzido por Alexandre NunesTeoria
Potência aparente
Vamos continuar estudando a potência em circuitos CA. No tópico anterior vimos que uma das fórmulas de potência média é:
Essa potência também é chamada de potência ativa ou potência real e também podemos escrevê-la assim:
Onde,
é chamada de potência aparente e é medida em volt-ampères ou VA. Além disso, adivinha, o termo também tem um nome! Esse termo é chamado de fator de potência (FP).
Muitos nomes novos né?! Calma, vamos fazer um exemplo para você fixar. No circuito abaixo, vamos determinar a potência aparente , o fator de potência e a impedância da carga .
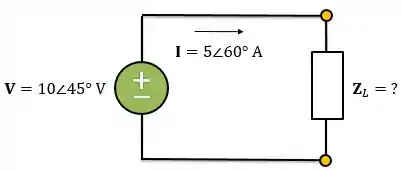
A potência aparente será:
Já o fator de potência será:
Quando o ângulo do fator de potência é negativo dizemos que o fator de potência está adiantado, porque a corrente está adiantada em relação à tensão.
Se o ângulo fosse positivo, o fator de potência estaria atrasado, porque a corrente estaria atrasada em relação à tensão.
Agora, precisamos calcular a impedância:
Como podemos ver, o ângulo do fator de potência é igual ao ângulo da impedância. Além disso, ele é negativo, o que indica que a carga é predominantemente capacitiva.
Também poderíamos confirmar isso analisando a forma retangular:
Como tem parte imaginária negativa consideramos que a carga é predominantemente capacitiva.
Vou fazer uma tabela esperta aqui para você não esquecer como é que funciona.
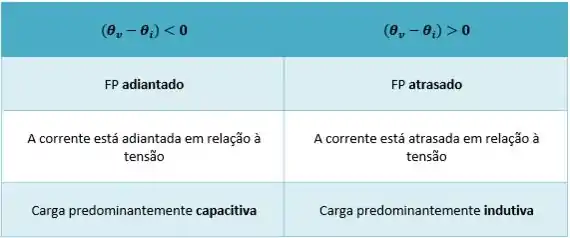
Potência complexa
Agora vamos juntar tudo o que a gente aprendeu. A potência complexa é importante porque ela contém praticamente todas as informações sobre a potência de um circuito. Como o próprio nome diz, ela é um número complexo e é definida da seguinte forma:
Onde e . Ou seja: a potência complexa que um carga absorve, é o produto da tensão com o conjugado da corrente
Passando para valores RMS:
Então, podemos escrever a equação acima assim:
Passando para forma retangular:
Como podemos ver, a parte real de é a potência ativa em watts. Além disso, chamamos a parte imaginária de potência reativa , na qual a unidade é VAR (volt-ampére reativo). Ou seja:
Além disso, podemos escrever a potência complexa em função da impedância complexa . Pela lei de Ohm
Multiplicando pelo conjugado da corrente nos dois lados da equação, temos:
Lembrando que , a equação acima fica assim:
Portanto, a potência ativa e reativa será:
Além disso:
Partiu fazer um exemplo!
No circuito abaixo, vamos determinar as potências complexa e aparente; as potências real e reativa; o fator de potência e a impedância da carga.
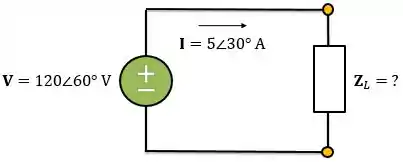
Passo 1:
Primeiro vamos passar a tensão e a corrente para seus valores RMS:
Então, aplicando a fórmula, a potência complexa será:
A potência aparente é o módulo da potência complexa:
Passo 2:
Agora vamos escrever a potência complexa na forma retangular:
Como , a potência ativa será:
Já a reativa:
Passo 3:
O ângulo do fator de potência é o ângulo da impedância. Então, vamos calcular primeiro. Pela lei de Ohm:
Portanto o fator de potência será:
Como o ângulo da impedância é positivo, ela é uma impedância indutiva. Logo, o FP é atrasado. Também poderíamos concluir isso vendo que a potência reativa é positiva.
Além disso, o ângulo da impedância é igual ao ângulo da potência complexa. Então, poderíamos ter calculado o fator de potência primeiro, utilizando o ângulo da potência complexa.
Beleza! Antes de continuar vou fazer um resumão do que estudamos:

Também é muito comum representar e na forma de um triângulo:
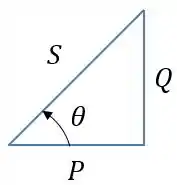
Esse triangulo é chamado de triângulo das potências e ajuda muito, pois sabendo as relações trigonométricas básicas chegamos à resposta sem precisar decorar fórmulas.
Potência complexa
Exercícios Resolvidos
Exercício Resolvido #1
Livro Sadiku, p.438, Problema 11.38
Para o sistema de potência da figura abaixo, determine:
- A potência média
- A potência reativa
- O fator de potência
Note que é um valor RMS.
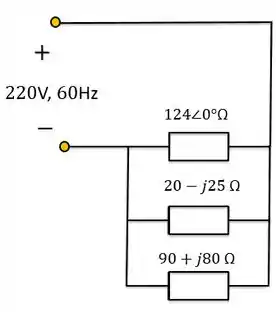
Passo 1
Para calcular a potência média, precisamos lembrar da fórmula:
Já foi fornecido o valor da tensão. Precisamos, então, calcular o valor da corrente que passa no circuito e o ângulo do fator de potência.
Passo 2
Para calcular a corrente que passa pelo circuito, vamos utilizar a Lei de Ohm:
No caso do circuito acima, como todas as impedâncias estão em paralelo, a tensão será:
Passo 3
Para calcular a corrente, falta ainda calcularmos a impedância equivalente do circuito. Como elas estão em paralelo:
Passo 4
Para finalizar o cálculo da impedância equivalente total, temos que fazer o cálculo do paralelo de com a impedância .
Lembrando que o ângulo do fator de potência é o ângulo da impedância, que, neste caso, será o da impedância total:
Passo 5
Finalmente, a corrente será:
Passo 6
Para calcular a potência média, colocamos os dados calculados na fórmula:
Passo 7
Por fim, precisamos calcular a potência reativa:
Se a gente analisar, o sinal da potência reativa deu negativo. Isso significa que a carga é predominantemente capacitiva.
Resposta
Exercício Resolvido #2
Livro Sadiku, p.438, Problema 11.41
Obtenha o fator de potência para cada um dos circuitos abaixo. Especifique se cada fator de potência está adiantado ou atrasado.
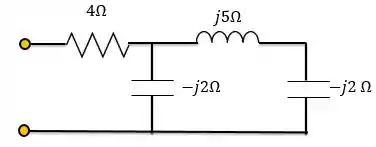
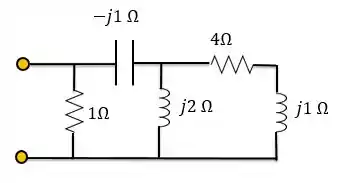
Passo 1
O fator de potência é o cosseno do ângulo da impedância equivalente do circuito. Logo, para o primeiro circuito, teremos que:
Passo 2
O fator e potência para o primeiro circuito, será, então:
Como o ângulo da impedância equivalente deu um número negativo, o fator de potência está adiantado. Ou seja: a carga é predominantemente capacitiva.
Passo 3
Para o próximo circuito, vamos fazer os cálculos em etapas:
Passo 4
Agora temos que calcular a impedância equivalente para a outra parte do circuito:
Passo 5
Finalmente:
Passo 6
O fator e potência para o segundo circuito, será, então:
Como o ângulo da impedância equivalente deu um número positivo, o fator de potência está atrasado. Ou seja: a carga é predominantemente indutiva.
Resposta
Primeiro circuito: FP = 0,554 adiantado
Segundo circuito: FP = 0,93 atrasado
Exercício Resolvido #3
Livro Sadiku, p.439, Problema 11.46
Para os fasores de tensão e corrente a seguir, calcule a potência complexa, a potência aparente, a potência real e a potência reativa. Especifique se o FP está adiantado ou atrasado.
Passo 1
Vamos começar pela letra a). Primeiro, vamos calcular a potência complexa, que é dada pela fórmula abaixo:
Passo 2
Como foi estudado na teoria, a potência complexa também pode ser escrita nesta forma:
Logo, passando a potência complexa calculada no passo acima para a forma retangular:
Então, já temos os valores das potências real e reativa:
Passo 3
Para vermos se o ângulo do fator de potência está adiantado ou atrasado, temos que analisar o ângulo da potência complexa, já que:
Então, analisando a potência complexa, podemos perceber que o ângulo do FP é:
Isso significa que o fator de potência está adiantado. Ou seja: a corrente está adiantada em em relação à tensão.
Passo 4
Para a letra b) faremos a mesma análise:
Passo 5
Passando a potência complexa calculada no passo acima para a forma retangular:
Então, já temos os valores das potências real e reativa:
Passo 6
Da mesma maneira, da potência complexa já é possível extrair o ângulo do FP:
Como o ângulo do fator de potência é um valor positivo, significa que o FP está atrasado. Ou seja: significa que a corrente está atrasada em 15° em relação à tensão.
Resposta
Exercício Resolvido #4
Livro Sadiku, p.439, Problema 11.51
Para o circuito inteiro abaixo, calcule:
O fator de potência. a potência média liberada pela fonte. a potência reativa. a potência aparente. a potência complexa.
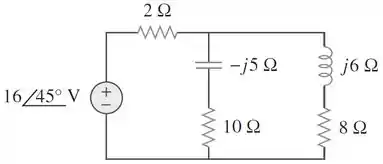
Passo 1
Vamos começar pela letra . O primeiro passo é encontrar a impedância equivalente do circuito. Já que o seu ângulo será o ângulo do fator de potência. A impedância equivalente desse circuito será:
Portanto, o fator de potência será:
Lembrando que o fator de potência é atrasado porque o seu ângulo é positivo.
Passo 2
Na letra temos que encontrar a potência média liberada pela fonte. Potência média é o mesmo que potência ativa e potência real, ou seja, é .
Agora para achar a potência média nós precisamos descobrir a potência total e ela será:
Com isso a potência total (ou aparente):
A fonte de está em RMS.
Passo 3
Para encontrar a potência reativa e aparente é só lembrar do triângulo das potências.
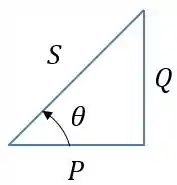
Com isso a potência reativa será:
Passo 4
Como , a potência aparente será:
Com isso a potência total (ou aparente), como foi efetuado o calculo no passo 2, temos
Passo 5
Como foi estudado na teoria, a potência complexa pode ser escrita nesta forma:
Logo, substituindo as potências calculadas nos passos acimas:
Resposta
Exercício Resolvido #5
Livro Sadiku, p.438, Problema 11.42
Uma fonte de 110 V RMS, 60 Hz é aplicada a uma impedância de carga . A potência aparente entrando na carga é de 120 VA com um fator de potência 0,707 atrasado.
- Calcule a potência complexa.
- Determine a corrente RMS fornecida para a carga.
- Determine .
- Supondo que , determine os valores de e .
Passo 1
A potência complexa tem a seguinte fórmula:
Sabemos que a potência aparente é 120 VA e sua formula é
Logo,
Além disso, o ângulo do fator de potência é o ângulo da potência complexa, então
Como o enunciado disse que o fator de potência é atrasado, a carga é predominantemente indutiva e o ângulo é positivo. Portanto,
Substituindo, temos que a potência complexa é
Passo 2
Para determinar a corrente é só aplicar a formula abaixo:
Como
Passo 3
Nós já sabemos o ângulo da impedância , já que ele é igual ao ângulo da potência complexa . Então, só falta a gente calcular o módulo da impedância. Pela lei de Ohm:
Substituindo os valores:
Logo a impedância será:
Passo 4
Agora, precisamos calcular os valores de e . Para isso, vamos passar a impedância para forma retangular:
Comparando com , temos:
Para terminar precisamos encontrar a frequência angular para substituirmos o seu valor e encontrar . Como a frequência da fonte é 60 Hz, temos:
Então, a indutância será:
Resposta
Exercício Resolvido #6
Livro Sadiku, Problema 11.44
Determine a potência complexa liberada por para o circuito da figura. Seja
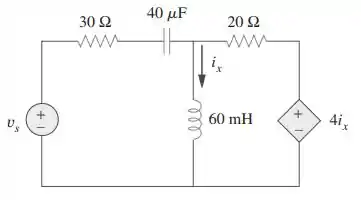
Passo 1
Vamos começar separando os dados:
Agora vamos calcular as impedâncias no domínio da frequência:
Para o indutor:
(lembrando que tudo tem que estar no Sistema Internacional)
Para o capacitor:
Passo 2
Agora vamos redesenhar o circuito com os valores encontrados no passo 1
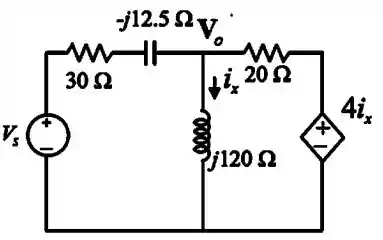
Passo 3
Vamos então aplicar a Lei das Correntes de Kirchhoff ao único nó do circuito (vamos chamar sua tensão de ) para encontrar o a partir da Lei de Ohm, veja:
Mas… quem é ?
Pela Lei de Ohm, , então, substituindo isso na equação anterior…
Passo 4
Agora, a corrente da fonte será:
Passo 5
Podemos então, calcular nossa potência complexa:
Resposta
Exercício Resolvido #7
Livro Sadiku, Problema 11.52
No circuito da figura, o dispositivo A recebe com, o dispositivo B recebe com, enquanto o dispositivo C é indutivo e consome e recebe .
(a) Determine o fator de potência para o sistema todo.
(b) Calcule dado que .
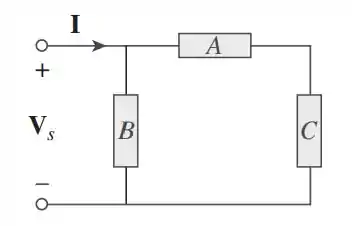
Passo 1
Vamos calcular nossas potências aparentes para cada dispositivo sabendo que .
A:
Então,
B:
C:
Passo 2
Somando tudo:
Passo 3
Agora vamos a letra (a)
O será:
(pois o ângulo é negativo)
Passo 4
E por fim, a letra (b)
Como
Sabemos que
Então,
Resposta
(a)
(b)
Exercício Resolvido #8
Livro Sadiku, Problema 11.39
Um motor CA com impedância é alimentado por uma fonte de
(a) Determine FP, P e Q.
(b) Determine o capacitor necessário para ser conectado em paralelo com o motor de modo que o fator de potência seja corrigido para a unidade.
Passo 1
Para calcular o FP, vamos primeiro passar a impedância para a forma polar para facilitar as contas:
Então, o Fator de Potência será:
Passo 2
Agora, para calcular as potências ativa (P) e reativa (Q), vamos primeiro achar a potência aparente (S):
, onde Z* é o conjugado, ou seja, basta trocar o sinal do ângulo (ou da parte imaginária)
Passando a potência aparente para a forma retangular, teremos
Sabemos que a Potência Ativa é a parte real e a Potência Reativa é a parte imaginária, então basta separar.
Passo 3
Para corrigir o Fator de Potência para FP =1, ou seja, Potência Reativa nula, vamos adicionar um banco de capacitores e é isso que queremos dimensionar; qual o tamanho do capacitor?
É assim:
, onde é a corrente do capacitor que é
E
Juntando as três, chegamos em , onde
Mas… quem é ?
Então,
Então, como
Resposta
(a)
(b)
Exercício Resolvido #9
Livro Sadiku, Problema 11.52
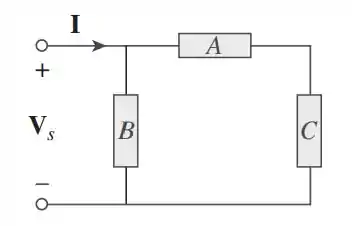
No circuito da figura, o dispositivo A recebe com, o dispositivo B recebe com, enquanto o dispositivo C é indutivo e consome e recebe .
(a) Determine o fator de potência para o sistema todo.
(b) Calcule dado que .
Passo 1
Vamos calcular nossas potências aparentes para cada dispositivo sabendo que .
A:
Então,
B:
C:
Passo 2
Somando tudo:
Passo 3
Agora vamos a letra (a)
O será:
(pois o ângulo é negativo)
Passo 4
E por fim, a letra (b)
Como
Sabemos que
Então,
Resposta
(a)
(b)
Exercício Resolvido #10
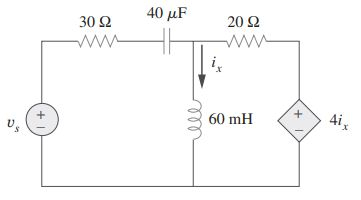
Livro Sadiku, Problema 11.44
Determine a potência complexa liberada por para o circuito da figura. Seja .
Passo 1
Vamos começar separando os dados:
Agora vamos calcular as impedâncias no domínio da frequência:
Para o indutor:
(lembrando que tudo tem que estar no Sistema Internacional)
Para o capacitor:
Passo 2
Agora vamos redesenhar o circuito com os valores encontrados no passo 1
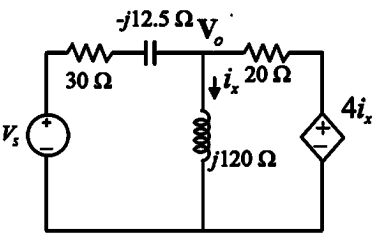
Passo 3
Vamos então aplicar a Lei das Correntes de Kirchhoff ao único nó do circuito (vamos chamar sua tensão de ) para encontrar o a partir da Lei de Ohm, veja:
Mas… quem é ?
Pela Lei de Ohm, , então, substituindo isso na equação anterior…
Passo 4
Agora, a corrente da fonte será:
Passo 5
Podemos então, calcular nossa potência complexa: