Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Circuitos RL

Ver Todos os Exercícios

Teoria

E aí, tranquilidade? Agora estudaremos os circuitos com resistores e indutores e vamos querer saber o que acontece com a tensão e corrente nesses elementos ao longo do tempo.

Vamos supor que a gente tenha o circuito abaixo e deseja-se calcular como resposta a corrente no indutor i para todo instante de tempo, como resolveríamos? É isso que vamos descobrir agora!

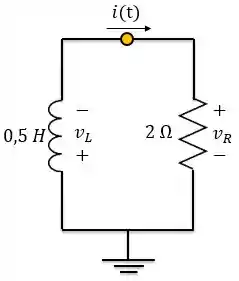
Circuito RL sem fonte

Esse circuito com resistor em série com o indutor, sem a presença de alguma fonte de tensão ou corrente ligada, é chamado de circuito RL sem fonte.

Para começar, a gente supõe que em t = 0 o indutor tem uma corrente inicial de 6   A , ou seja:

i 0 = 6   A

Agora, vamos aplicar a LTK, no circuito acima:

v L + v R = 0

Como a gente sabe que

v L = L d i d t = 0,5 d i d t

e

v R = R i = 2 i

Substituindo:

0,5 d i d t + 2 i = 0

Essa equação é uma EDO de primeira ordem. Você lembra como resolvê-la?

Para resolver essa equação, primeiro vamos obter a equação característica:

0,5 r + 2 = 0

r = - 2 0,5

r = - 4

Sabemos que a solução geral da equação é dada por:

i t = A e r t

Sendo A uma constante.

Substituindo o valor de r encontrado, temos:

i t = A e - 4 t

Agora, a gente tem que encontrar o valor da constante A . Lembra lá no início que o indutor tem uma corrente inicial de 6   A ? Então, utilizaremos essa condição inicial aqui:

i 0 = 6 = A e - 4 ( 0 )

Logo,

A = 6

Beleza! Então nossa solução final é:

i t = 6 e - 4 t     A ,     p a r a   t ≥ 0

Essa solução é chamada de resposta natural do circuito, pois ela só depende da energia armazena inicialmente no indutor e dos valores dos elementos do circuito.

Agora, vamos analisar o gráfico da resposta natural.

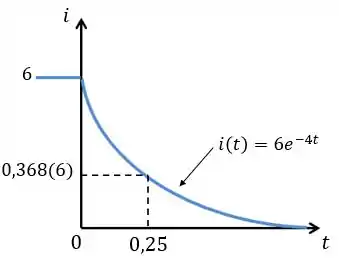
A gente vê que a corrente inicial decresce exponencialmente até chegar a zero. Assim como o circuito RC, o circuito RL também possui constante de tempo (τ).

Por definição, a constante de tempo (τ) de um circuito é o tempo necessário para que a corrente caia a 36,8% do seu valor inicial. Ou seja, para o nosso circuito, a constante de tempo seria 0,25   s .

τ = 0,25   s

Se a gente voltar nas equações, veremos que o valor de τ pode ser obtido dividindo o valor da indutância pela resistência:

L R = 0,5 2 = 0,25

Logo, para o circuito RL, a constante de tempo também depende exclusivamente do valor dos elementos passivos.

τ = L R

Vamos relembrar os passos até aqui:

  1. Circula no indutor uma corrente inicial:

    2. i 0 = I 0

  2. Aplicando LTK chegamos à EDO:

    3. L d i d t + R i = 0

  3. Resolvendo a EDO:

    4. i t = A e - R t L

  4. Encontrar A a partir da condição inicial:

    5. A = i 0 = I 0

  5. Encontramos a resposta natural do circuito:

    6. i t = I 0 e - R t L = I 0 e - t τ

  6. E a constante de tempo:

τ = L R

Resposta ao degrau, impulso e rampa

Agora vamos estudar a resposta do circuito quando há a presença de fontes de corrente ou tensão. Muitas vezes essas fontes podem ser descritas pelas funções singulares, como a função degrau, impulso ou rampa.

Começaremos pela função degrau unitário, que tem essa cara aqui:

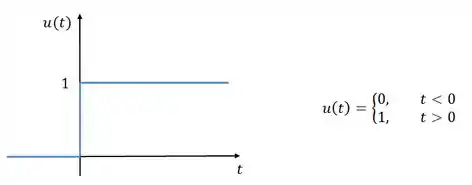
Vamos encontrar a resposta ao degrau unitário no circuito abaixo:

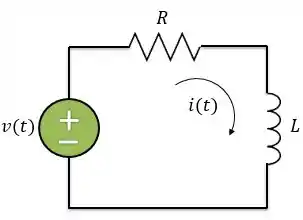
O que queremos, então, é encontrar a corrente i ( t ) sendo a fonte de corrente um degrau unitário v t = u ( t ) . Para isso, vamos seguir esses passos:

1º PASSO: Como a fonte de tensão é um degrau unitário, até o instante t = 0 , não há circulação de corrente no circuito. Logo, i t = 0 para t < 0 . Lembrando que a corrente no indutor não pode variar instantaneamente, então:

i 0 - = i 0 = i 0 + = 0

2º PASSO: Agora, vamos aplicar a Lei das tensões de Kirchhoff.

v = v R + v L

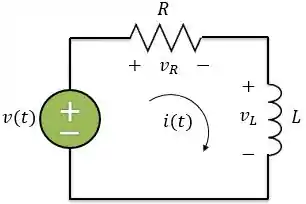
Sendo

v R = R i

e

v L = L d i d t

Como para t > 0 o valor da fonte de tensão é igual a 1 , temos:

1 = R i + L d i d t

3º PASSO: Chegamos a uma EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.

i t = i h ( t ) + i p ( t )

Primeiro, vamos resolver a homogênea:

L d i h d t + R i h = 0

Nós já resolvemos essa EDO quando estudamos o caso sem fontes e vimos que resposta é:

i h t = A e - R t L

Agora, precisamos encontrar a solução particular.

L d i p d t + R i p = 1

Como 1 é uma constante, a solução particular deve ser também uma constante:

i p t = B ,

sendo B uma constante.

Substituindo, temos:

L d ( B ) d t + R ( B ) = 1

Como a derivada de uma constante é zero:

B = 1 R

Portanto, a solução geral é:

i t = A e - R t L + 1 R

4º PASSO: Calma, estamos quase lá! Para terminar, precisamos encontrar o valor da constante A . Para isso vamos utilizar a nossa condição inicial i 0 + = 0 .

0 = A e - R 0 L + 1 R

A = - 1 R

Substituindo:

i t = - 1 R e - R t L + 1 R

i t = 1 R 1 - e - R t L

Logo, a corrente no indutor para qualquer instante de tempo será:

i t = 0 ,                                                                         t < 0         1 R 1 - e - R t L ,                         t > 0      

Outra maneira de escrever seria:

i t = 1 R 1 - e - R t L u ( t )

Graficamente a resposta ao degrau será assim:

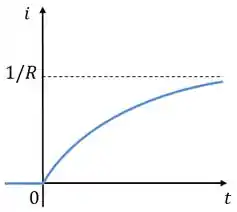
Vamos supor agora que a fonte de corrente v ( t ) é um impulso unitário δ ( t ) .

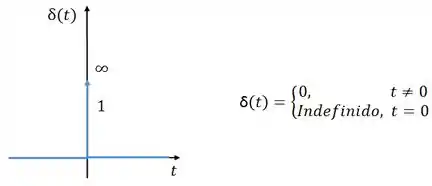
Então, quando v t = δ t , a tensão da fonte só não é zero em t = 0 . Logo, para t > 0 a fonte de tensão pode ser substituída por um curto-circuito, tornando o circuito igual ao caso sem fonte.

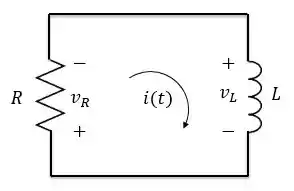
No qual já sabemos a solução:

i t = A e - R t L

No instante t = 0 , um impulso de tensão no resistor causaria uma corrente infinita passando pelo indutor, o que não é possível. Logo, o impulso de tensão deve ser aplicado no indutor.

Agora se liga nesse teorema aqui: Um impulso unitário de tensão no indutor altera instantaneamente sua corrente de zero para 1 / L   ampéres. Portanto:

i 0 + = 1 L

Sabendo disso, já podemos calcular a constante A .

1 L = A e -   R ( 0 ) L

A = 1 L

Portanto, a resposta ao impulso unitário será:

i t = 1 L e -   R t L   u ( t )

Para terminar, vamos analisar quando a fonte de tensão   v t for a rampa unitária r ( t ) . A gente obtém a rampa unitária integrando a função degrau unitário:

r t = ∫ - ∞ t u t   d t = t   u ( t )

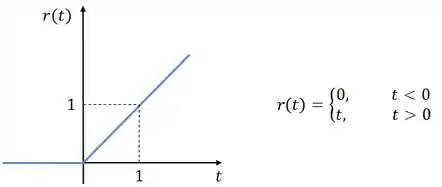
Portanto, se a gente integrar a resposta ao degrau unitário, encontraremos a resposta à rampa unitária. Logo:

i t = ∫ 0 t 1 R 1 - e - R L λ   d λ

i t = ∫ 0 t 1 R d λ - ∫ 0 t 1 R e - R L λ   d λ

i t = 1 R λ t 0 + L R 2 e - R L λ t 0

i t = 1 R t + L R 2 e - R L t - L R 2

i t = 1 R t + L R 2 e - R L t - 1 ,           p a r a   t > 0

Pronto, muita coisa, né? Mas relaxa, separei uns exercícios bacanas para você arrebentar! ;)

Resposta ao degrau, impulso e rampa

Exercícios Resolvidos

Exercício Resolvido #1

Livro Sadiku, p.267, Problema 7.14

Calcule a constante de tempo do circuito abaixo

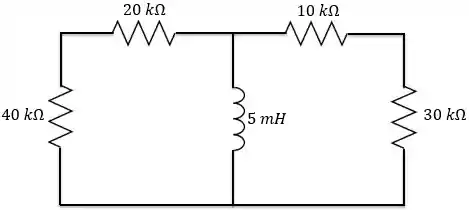
Passo 1

O circuito acima possui um indutor e vários resistores. Para encontrarmos o valor da constante de tempo, precisamos transformar esse circuito no circuito RL sem fonte que conhecemos.

Passo 2

Para isso, vamos calcular a resistência equivalente de Thévenin nos terminais do indutor.

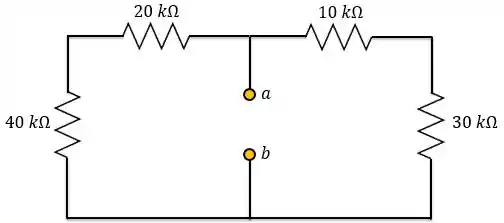
Fazendo a associação em série dos resistores:

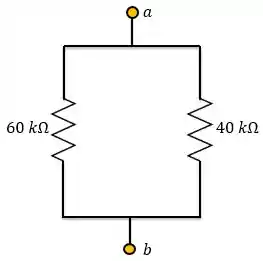
Passo 3

Como esses resistores estão associados em paralelo:

R T h = 60 × 40 60 + 40

R T h = 2400 100 = 24   k Ω  

Passo 4

Pronto, agora que encontramos R T h , chegamos ao nosso circuito RL sem fonte, com apenas um resistor e um indutor.

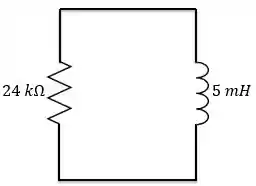
A gente conhece a constante de tempo para esse circuito.

τ = L R

Substituindo os valores:

τ = 5 × 10 - 3 24 × 10 3

τ = 0,2083   µ s

Resposta

τ = 0,2083   µ s

Exercício Resolvido #2

Introdução a análise de circuitos - Robert L Boylestad – Ed. 12 – Exercício 11.11

Para o circuito da figura, composto de valores padrão:

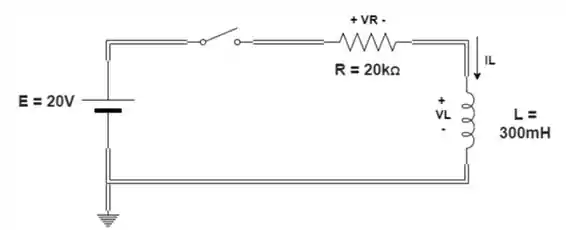
  1. Determine a constante de tempo.
  2. Escreva a expressão matemática para a corrente i L após a chave ser fechada.
  3. Repita o item (b) para v L e v R .
  4. Determine v L e i L em uma, três e cinco constantes de tempo.

Passo 1

A constante de tempo para o circuito RL é dada pela fórmula:

τ = L R

τ = 300 m 20 k

τ = 15 * 10 - 6 s

Passo 2

Após a chave ser fechada, no caso do indutor, a corrente i L irá aumentar de acordo com a fórmula:

i L =   E R * ( 1 - e - t τ )

i L =   20 20 k * ( 1 - e - t 15 * 10 - 6 )

i L =   0,001 * ( 1 - e - t 15 * 10 - 6 )

Passo 3

Vamos calcular a tensão no indutor após o fechamento da chave, ela irá decrescer ao longo do tempo:

V L =   E * e - t τ

V L =   20 * e - t 15 * 10 - 6

Passo 4

Se a tensão do indutor está decrescendo, a tensão no resistor irá aumentar ao longo do tempo:

V R =   E * ( 1 - e - t τ )

V R =   20 * ( 1 - e - t 15 * 10 - 6 )

Passo 5

Vamos calcular V L e i L segundo as seguintes equações:

V L =   E * e - t τ

i L =   E R * ( 1 - e - t τ )

Para t =   τ :

V L =   20 * e - τ τ = 20 * e - 1

V L = 7,36 V

i L = 0,001 * 1 - e - τ τ = 0,001 * 1 - e - 1

i L = 0,63 m A

Para t =   3 τ :

V L =   20 * e - 3 τ τ = 20 * e - 3

V L = 0,996 V

i L = 0,001 * 1 - e - 3 τ τ = 0,001 * 1 - e - 3

i L = 0 , 95 m A

Para t =   5 τ :

V L =   20 * e - 5 τ τ = 20 * e - 5

V L = 0,13 V

i L = 0,001 * 1 - e - 5 τ τ = 0,001 * 1 - e - 5

i L = 0,99 m A

Resposta

a)

τ = 15 * 10 - 6 s

b)

i L =   0,001 * ( 1 - e - t 15 * 10 - 6 )

c)

V L =   20 * e - t 15 * 10 - 6

V R =   20 * ( 1 - e - t 15 * 10 - 6 )

d)

Para t =   τ :

V L = 7,36 V

i L = 0,63 m A

Para t =   3 τ :

V L = 0,996 V

i L = 0,95 m A

Para t =   5 τ :

V L = 0,13 V

i L = 0,99 m A

Exercício Resolvido #3

Introdução a análise de circuitos - Robert L Boylestad – Ed. 12 – Exercício 11.13

Dada a fonte de 18V, use os valores padrão para projetar um circuito com a resposta da figura:

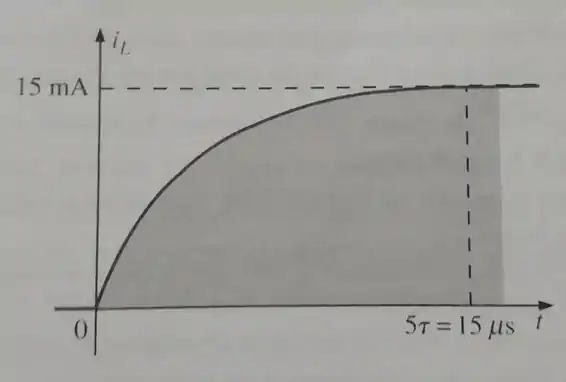
Passo 1

Pelo que foi dito no enunciado já sabemos que E = 18 V . E que a constante de tempo é igual a:

5 τ = 15 μ s

τ = 3 μ s

Passo 2

Sabemos que a corrente máxima que circula pelo indutor é quando t = 5 τ e segue a fórmula:

i L =   E R * 1   -   e - 5 τ τ = 15 m A

Substituindo os valores que já sabemos:

18 R 1   -   e - 5 = 15 m

R =   18 15 * 10 - 3 1 - e - 5 = 1200

R = 1,2 k Ω

Passo 3

Como sabemos que a constante de tempo segue a fórmula:

τ =   L R

3 μ =   L 1,2 k

L = 3 μ * 1,2 k = 3,6 m H

Resposta

R = 1,2 k Ω

L = 3,6 m H

Exercício Resolvido #4

Livro Sadiku, p.267, Problema 7.13

Determine R ,   L e τ no circuito abaixo

v t = 80 e - 10 3 t   V   ,               t > 0

i t = 5 e - 10 3 t   m A   ,               t > 0

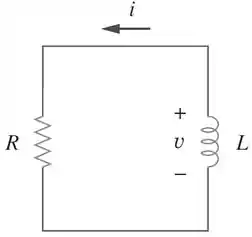
Passo 1

O circuito acima é um circuito RL sem fonte. Precisamos encontrar os valores da resistência, da indutância e da constante de tempo. A gente viu na teoria que a corrente nesse circuito tem a seguinte relação geral:

i t = I 0 e - R t L = I 0 e - t τ

Passo 2

A corrente nesse circuito é dada no enunciado:

i t = 5 e - 10 3 t   m A

Comparando as equações a gente pode ver que:

R L = 10 3

Como

τ = L R = 1 10 3

τ = 1   m s

Passo 3

Já encontramos a constante de tempo. Agora, vamos encontrar o valor de R .

Vamos utilizar a famosa lei de Ohm:

V = R i

80 e - 10 3 t = R × 5 e - 10 3 t × 10 - 3

R = 80 e - 10 3 t 5 e - 10 3 t × 10 - 3

R = 80 0,005

R = 16000 = 16   k Ω

Passo 4

Agora precisamos calcular o valor de L . Sabemos que

τ = L R = 1 10 3

Então:

L = R × 1 10 3

Como R = 16   k Ω

L = 16 × 10 3 × 1 10 3

L = 16   H

Resposta

R = 16   k Ω

L = 16   H

τ = 1   m s

Exercício Resolvido #5

Livro Sadiku, p.268, Problema 7.22

Determine i ( t ) e v ( t ) para t > 0 no circuito abaixo se i 0 = 10   A .

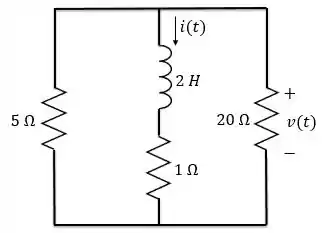
Passo 1

O circuito acima possui um indutor e vários resistores. Precisamos transformá-lo no circuito RL sem fonte com apenas um resistor e um indutor, para encontrarmos a corrente i ( t ) e a tensão v ( t ) .

Passo 2

Para isso, vamos calcular a resistência equivalente de Thévenin nos terminais do indutor.

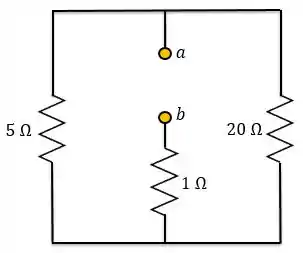
Vamos ajeitar o circuito para visualizar melhor e ajudar a gente.

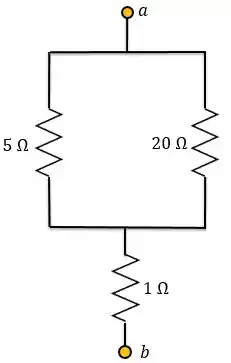
Passo 3

Logo, a gente vê que o resistor de 1 Ω está em série com a associação em paralelo dos resistores de 5 Ω e 20 Ω .

R T h = ( 5 20 ) + 1

R T h = 5 × 20 5 + 20 + 1

R T h = 5   Ω  

Passo 4

Pronto, agora que encontramos R T h , chegamos ao nosso circuito RC sem fonte, com apenas um resistor e um indutor.

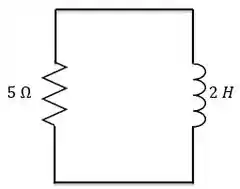
A gente conhece a constante de tempo para esse circuito.

τ = L R

Substituindo os valores:

τ = 2 5

Passo 5

A gente viu na teoria que a corrente nesse circuito tem a seguinte relação geral:

i t = I 0 e - R t L = I 0 e - t τ

Onde i 0 = I 0 = 10   A

Logo,

i t = 10 e - 5 2 t

i t = 10 e - 2,5 t   A

Passo 6

Aplicando divisor de corrente, a gente encontra a corrente que passa pelo resistor de 20   Ω .

i 2 = 5 5 + 20   × - i

Esse sinal de menos apareceu na corrente i , pois a gente inverteu o seu sentido, originalmente ela estava saindo do nó, mas para o cálculo do divisor de corrente consideramos ela entrando no nó.

i 2 = 5 25 × - 10 e - 2,5 t

i 2 = - 2 e - 2,5 t   A

Passo 7

Agora é só aplicar a boa e velha lei de Ohm para encontrarmos a tensão v ( t ) .

v t = 20 i 2

v t = 20 × - 2 e - 2,5 t

v t = - 40 e - 2,5 t   V

Resposta

i t = 10 e - 2,5 t   A

v t = - 40 e - 2,5 t   V

Exercício Resolvido #6

Livro Sadiku, p.271, Problema 7.53

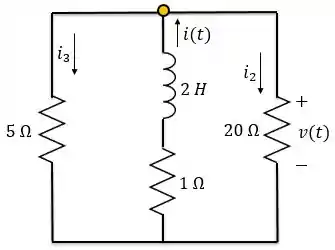
Determine a corrente i ( t ) no indutor para t < 0 e t > 0 no circuito abaixo.

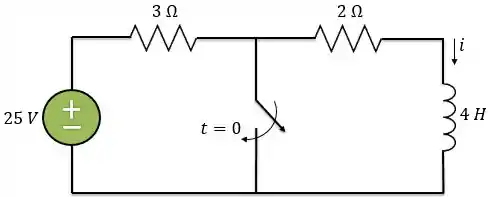
Passo 1

No circuito acima temos uma chave. Em t = 0 essa chave muda de posição, ou seja, para t < 0 a chave está aberta, enquanto para t > 0 a chave está fechada. Vamos encontrar a corrente i t , que passa pelo indutor nesses dois casos.

Passo 2

Primeiro, vamos calcular a corrente quando a chave está aberta. Para t < 0 o circuito pode ser redesenhado assim:

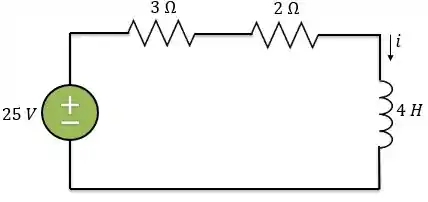
Considerando que o circuito estava funcionando no regime permanente. Sabemos que o indutor é um curto-circuito em corrente contínua. Logo a corrente para t < 0 , pode ser obtida no circuito abaixo:

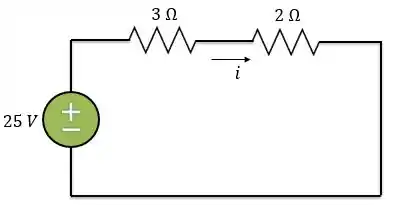
Pela lei de Ohm:

i t = 25 3 + 2

i t = 5   A

Passo 3

Agora vamos analisar o circuito quando a chave se fecha. Para t > 0 a circuito fica assim:

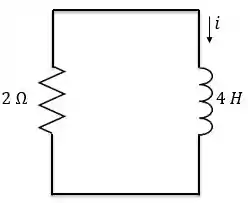
Esse circuito a gente está careca de saber. É o circuito RL sem fonte. Sabemos que a corrente nesse circuito se comporta assim:

i t = i ( 0 ) e - R L t

Passo 4

Nós temos os valores de R e L , precisamos só encontrar o valor da corrente no instante t = 0 . Para isso, temos que lembrar que a corrente no indutor não pode variar instantaneamente.

i 0 - = i 0 = i 0 +

Em t = 0 - , a chave está na iminência de se fechar, mas ainda está aberta. Logo, o valor da corrente nesse instante é o mesmo de t < 0 .

i 0 - = 5   A

Logo,

i 0 = 5   A

Substituindo todos os valores que temos, chegamos a seguinte corrente para t > 0 .

i t = 5 e - 2 4 t   A

i t = 5 e - 0,5 t   A

Resposta

i t = 5   ,                                       t < 0 5 e - 0,5 t ,     t > 0

Exercício Resolvido #7

Introdução a análise de circuitos - Robert L Boylestad – Ed. 12 – Exercício 11.18

Considerando o circuito da figura:

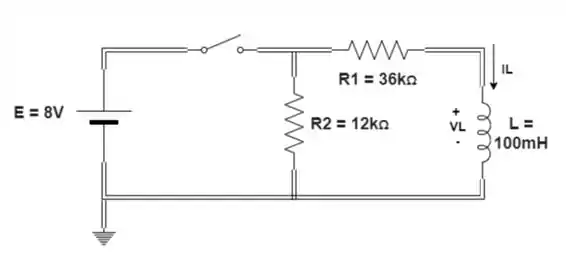
  1. Determine as expressões matemáticas para a corrente i L e para a tensão v L quando a chave é fechada.
  2. Repita o item (a) se a chave for aberta após a passagm de cinco constantes de tempo.

Passo 1

Primeiro devemos calcular o equivalente Thévenin entre o terminais do indutor, para isso devemos substituir a fonte de tensão por um curto circuito:

R t h = 12 k * 0 12 k + 0 + 36 k = 36 k Ω

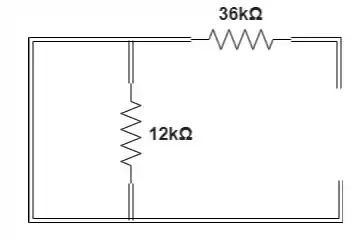
Enquanto a tensão E é igual a tensão a fonte 8V.

Passo 2

Podemos calcular a constante de tempo para o momento de carregamento τ :

τ = L R t h = 100 m 36 k = 2,78 μ s

Passo 3

Após a chave ser fechada, a corrente que circula pelo indutor é dada pela fórmula:

i L =   E R t h   1 - e - t τ

i L =   8 36 k   1 - e - t 2,78 μ

i L =   0,22   ( 1 - e - t 2,78 μ ) m A

Passo 4

A tensão sobre o indutor, v L segue a equação:

v L = E *   e - t τ

v L = 8 *   e - t 2,78 μ

Passo 5

Após 5 constantes de tempo, o indutor irá descarregar a partir de um valor inicial igual a:

v i L =   - ( v R 1   +   v R 2 )

v i L =   - ( i 1 * R 1   +   i 2 * R 2   )

v i L =   - i L R 1   +   R 2   =   - E R 1   ( R 1   +   R 2   )

v i L = - 8 36 k 36 k +   12 k =   - 10,67 V

Passo 6

A nova constante de tempo τ ' para o circuito enquanto o indutor descarrega é:

τ ' =   L R e q =   100 m ( 36 k + 12 k ) = 2,08 μ s

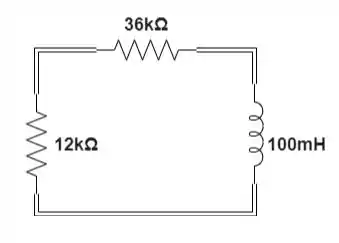
Passo 7

A tensão v L   sobre o indutor descarregando segue a fórmula, onde já calculamos o valor inicial de v i L :

v L =   - v i L * ( 1 - e - t τ ' )

v L =   10,67 * ( 1 - e - t 2,08 μ )

Passo 8

A corrente i L que passa pelo indutor segue a fórmula:

i L =   E R 1   e - t τ '

i L =     8 36 k   e - t 2,08 μ

i L = 0,22   e - t 2,08 μ m A

Resposta

a)

i L =   0,22   1 - e - t 2,78 μ m A

v L = 8 * ( e - t 2,78 μ ) V

b)

i L = 0,22   e - t 2,08 μ m A

v L =   10,67 * 1 - e - t 2,08 μ V

Exercício Resolvido #8

Livro Sadiku, p.271, Problema 7.55

Determine v ( t ) para t < 0 e t > 0 no circuito abaixo.

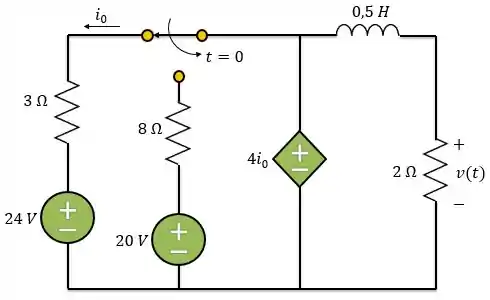
Passo 1

Vamos começar! Nesse circuito temos uma chave. Em t = 0 essa chave muda de posição, ou seja, para t < 0 a chave está na posição horizontal como está desenhado no circuito acima. Já para t > 0 a chave muda de posição e se conecta com o resistor de 8   Ω .

Passo 2

Vamos encontrar a tensão v t , que é aplicada no indutor nesses dois casos.

Primeiro, vamos calcular a tensão para t < 0 . Neste caso o circuito pode ser redesenhado assim:

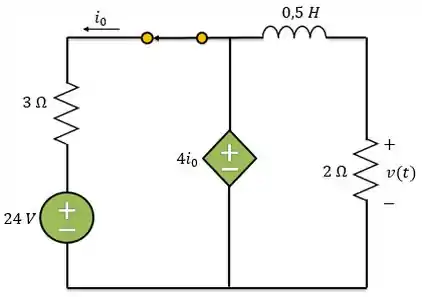
Considerando que o circuito estava funcionando no regime permanente. Sabemos que o indutor é um curto-circuito em corrente contínua.

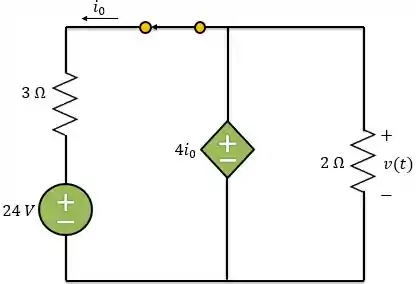
Logo, a tensão v ( t ) para t < 0 , tem o valor da fonte de tensão dependente, já que a fonte está em paralelo com o resistor de 2   Ω .

v t = 4 i 0

Passo 3

Precisamos, então, descobrir o valor de i 0 . Aplicando a LTK na malha da esquerda do circuito acima, temos:

3 i 0 + 24 - 4 i 0 = 0

i 0 = 24   A

Logo,

v t = 4 × 24

v t = 96   V

Encontramos o valor da tensão, mas antes de analisarmos o circuito para t > 0 , vamos calcular a corrente i que passa pelo indutor e pelo resistor de 2   Ω . Esse resultado vai nos ajudar ali na frente.

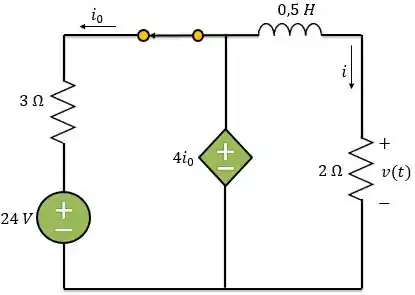
Pela lei de Ohm

i t = 96 2 = 48   A

Passo 4

Agora vamos analisar o circuito para t > 0 . Para este caso, podemos considerar fonte dependente de tensão desligada, ou seja, um curto-circuito. Pois essa fonte depende de i 0 , e esta corrente é zero para este caso.

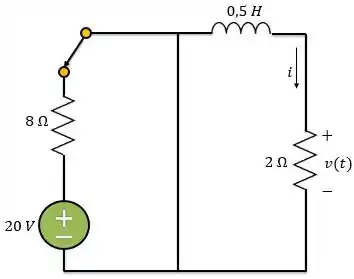
Devido a esse curto-circuito, o circuito a cima pode ser dividido em dois, como queremos encontrar v ( t ) , vamos analisar o lado direito do circuito.

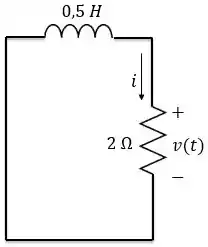
Esse circuito a gente conhece. É o circuito RL sem fonte. Sabemos que a corrente nesse circuito se comporta assim:

i t = i ( 0 ) e - R L t

Passo 5

Nós temos os valores de R e L , precisamos só encontrar o valor da corrente no instante t = 0 . Para isso, temos que lembrar que a corrente no indutor não pode variar instantaneamente.

i 0 - = i 0 = i 0 +

Em t = 0 - , a chave está na iminência de mudar de posição, mas ainda está aberta. Logo, o valor da corrente nesse instante é o mesmo de t < 0 .

i 0 - = 48   A

Logo,

i 0 = 48   A

Substituindo todos os valores que temos, chegamos a seguinte corrente para t > 0 .

i t = 48 e - 2 0,5 t   A

i t = 48 e - 4 t   A

Agora é só aplicar a lei de Ohm para encontrarmos a tensão v ( t ) para t > 0 .

v t = 2 × i t

v t = 2 × 48 e - 4 t

v t = 96 e - 4 t   V

Resposta

v t = 96   ,                                       t < 0 96 e - 4 t ,                       t > 0

Exercício Resolvido #9

Livro Sadiku, p.271, Problema 7.65

Se o pulso de entrada do gráfico abaixo for aplicado ao circuito, determine a resposta i ( t ) .

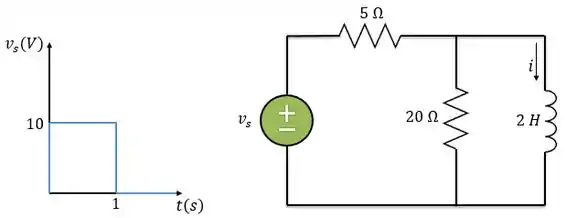
Passo 1

Precisamos encontrar a corrente no indutor i t quando a fonte de tensão v s tiver aquela forma apresentada no gráfico. A gente pode descrever esse pulso de entrada como uma fonte de 10   V que foi ligada em t = 0 e uma fonte de - 10   V que foi ligada mais tarde, em t = 1 .

v s = 10 u t - u t - 1

Passo 2

Agora, vamos analisar no intervalo de 0 < t < 1 . Nesse intervalo a fonte de tensão vale 1 0   V . Vamos analisar o circuito abaixo para encontrarmos a corrente nesse intervalo.

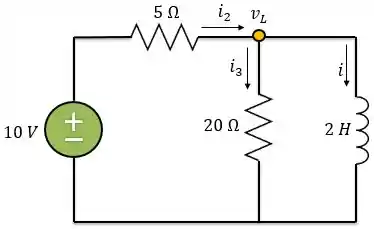
Primeiro, vamos aplicar a LCK ao nó:

i 2 = i 3 + i

Sabemos que a tensão no indutor tem a seguinte relação:

v L = L d i d t = 2 d i d t

E como o indutor está em paralelo com o resistor de 20   Ω , eles possuem a mesma tensão.

v L = 20 i 3

v L = 20 ( i 2 - i )

Agora, vamos escrever a corrente i 2 em função da tensão nodal v L .

i 2 = 10 - v L 5

Substituindo,

v L = 20 10 - v L 5 - i

v L = 200 5 - 20 5 v L - 20 i

v L = 40 - 4 v L - 20 i

5 v L + 20 i = 40

Como,

v L = 2 d i d t

Substituindo,

5 × 2 d i d t + 20 i = 40

10 d i d t + 20 i = 40

Passo 3

Chegamos a uma EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.

i t = i h ( t ) + i p ( t )

Primeiro, vamos resolver a homogênea:

10 d i h d t + 20 i h = 0

Nós já resolvemos essa EDO quando estudamos o caso sem fontes e vimos que resposta é:

i h t = A e - 2 t

Agora, precisamos encontrar a solução particular.

10 d i p d t + 20 i p = 40

Como 3 é uma constante, a solução particular deve ser também uma constante:

i p t = B ,

sendo B uma constante.

Substituindo, temos:

10 d ( B ) d t + 20 ( B ) = 40

Como a derivada de uma constante é zero:

B = 2

Portanto, a solução geral é:

i t = A e - 2 t + 2

Passo 4

Agora, precisamos encontrar o valor da constante A . Até o instante t = 0 , não há circulação de corrente no circuito. Logo, i 0 = 0 . Lembrando que a corrente no indutor não pode variar instantaneamente, então:

i 0 - = i 0 = i 0 + = 0

Então, utilizando a nossa condição inicial

0 = A e - 2 × ( 0 ) + 2

A = - 2

Substituindo:

i t = - 2 e -   2 t + 2     A

Logo, a corrente no indutor para 0 < t < 1 será:

i t = 2 ( 1 - e -   2 t )     A

Passo 5

Agora temos que calcular i t para t > 1 .

Como a tensão da fonte passa a ser zero para t > 1 , a fonte de tensão pode ser substituída por um curto-circuito, tornando o circuito igual ao caso sem fonte.

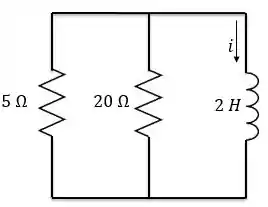
Fazendo a associação em paralelo dos resistores, temos:

R e q = 20 × 5 20 + 5

R e q = 100 25 = 4   Ω

Chegando nesse circuito RL sem fonte simples.

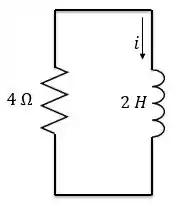
Aqui a gente tem que ter um cuidado especial, pois a nossa condição inicial é em t = 1 . Então, temos que considerar esse deslocamento no tempo.

i t = i 1 e - 2 ( t - 1 )

Passo 6

Como a corrente no indutor não pode variar instantaneamente, ou seja:

i 1 - = i 1 = i 1 +

Para instante t = 1 - , temos a expressão da corrente, que foi aquele calculado em 0 < t < 1 . Logo:

i 1 - = 2 ( 1 - e -   2 ( 1 ) )

i 1 - = 2 × ( 1 - 0,1353 )

i 1 - = 1.7294   A

Logo, a corrente no indutor para t > 1 será:

i t = 1.729 4 e - 2 t - 1   A

Resposta

i t = 2 ( 1 - e -   2 t ) ,               0 < t < 1 1.729 4 e - 2 t - 1 ,                     t > 1

Exercício Resolvido #10

Livro Close, p.159, Problema 3.12

Determine as respostas ao degrau unitário e ao impulso no circuito abaixo.

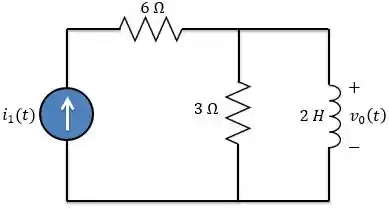
Passo 1

O enunciado nos pede a tensão no indutor v 0 t quando a corrente da fonte i 1 ( t ) for primeiro um degrau unitário   u t e depois um impulso unitário δ ( t ) . Vamos começar!

Passo 2

Primeiro, vamos analisar o caso em que i t = u t . Como a fonte de corrente é um degrau unitário, até o instante t = 0 , não há circulação de corrente no circuito e para t > 0 a fonte de corrente vale 1   A . Logo, para t > 0 ,   vamos analisar o circuito abaixo.

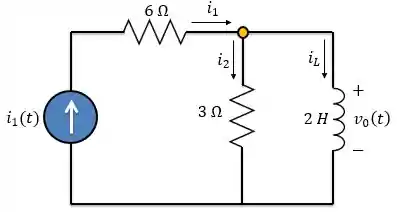
Sabemos que a tensão no indutor tem a seguinte relação:

v 0 t = L d i L d t = 2 d i L d t

E como o indutor está em paralelo com o resistor de 3   Ω , eles possuem a mesma tensão.

v 0 t = 3 i 2

Aplicando LCK no nó:

i 1 = i 2 + i L

Como, para t > 0 , i 1 = 1   A .

i 2 = 1 - i L

Logo,

v 0 t = 3 ( 1 - i L )

2 d i L d t = 3 - 3 i L

2 d i L d t + 3 i L = 3

Passo 3

Chegamos a uma EDO não homogênea. A solução geral dessa equação é composta pela solução particular mais a solução da homogênea.

i L t = i h ( t ) + i p ( t )

Primeiro, vamos resolver a homogênea:

2 d i h d t + 3 i h = 0

Nós já resolvemos essa EDO quando estudamos o caso sem fontes e vimos que resposta é:

i h t = A e - 3 2 t

Agora, precisamos encontrar a solução particular.

2 d i p d t + 3 i p = 3

Como 3 é uma constante, a solução particular deve ser também uma constante:

i p t = B ,

sendo B uma constante.

Substituindo, temos:

2 d ( B ) d t + 3 ( B ) = 3

Como a derivada de uma constante é zero:

B = 3 3 = 1

Portanto, a solução geral é:

i L t = A e - 3 2 t + 1

Passo 4

Agora, precisamos encontrar o valor da constante A . Como a fonte de corrente é um degrau unitário, até o instante t = 0 , não há circulação de corrente no circuito. Logo, i L t = 0 para t < 0 . Lembrando que a corrente no indutor não pode variar instantaneamente, então:

i 0 - = i 0 = i 0 + = 0

Então, utilizando a nossa condição inicial

0 = A e - 3 2 × ( 0 ) + 1

A = - 1

Substituindo:

i L t = 1 - e -   3 2 t   A

Logo, a corrente no indutor para qualquer instante de tempo será:

i L t = 0 ,                                                                         t < 0         1 - e -   3 t 2 ,                                           t > 0      

Também podemos escrever assim:

i L t = 1 - e -   3 2 t u ( t )

Passo 5

Agora que encontramos a corrente que passa pelo indutor, finalmente podemos encontrar o valor de v 0 t . Sabemos que:

v 0 t = 2 d i L d t

Substituindo,

v 0 t = 2 × d 1 - e -   3 2 t d t

v 0 t = 2 × - 3 2 - e -   3 2 t

Logo,

v 0 t = 3 e -   3 2 t   u ( t )

Também poderíamos encontrar v 0 t , pela equação de tensão no resistor.

v 0 t = 3 ( 1 - i L )

Substituindo i L :

v 0 t = 3 1 - 1 - e -   3 2 t

v 0 t = 3 e -   3 2 t   u t

Viu só!

Passo 6

Agora, precisamos encontrar v 0 t para quando i i t = δ ( t ) . No instante t = 0 , um impulso de corrente no indutor causaria uma corrente infinita passando por ele, o que não é possível. Logo, o impulso de corrente fornecido pela fonte deve passar somente pelos resistores.

Quando esse impulso unitário de corrente passa pelo resistor de 3   Ω , ele gera um impulso de tensão no resistor e, consequentemente, no indutor, já que eles estão em paralelo. Portanto podemos dizer que:

v 0 t = 3 δ ( t )

Passo 7

Encontramos o valor de v 0 no instante t = 0 . Agora temos que calcular para t > 0 .

Como a corrente da fonte é zero para t > 0 , a fonte de corrente pode ser substituída por um circuito aberto, tornando o circuito igual ao caso sem fonte.

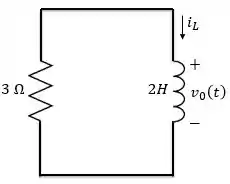
Já sabemos que a corrente para esse circuito tem a seguinte valor:

i L t = i L 0 e - 3 2 t  

Agora, lembra daquele teorema que um impulso unitário de tensão no indutor altera instantaneamente sua corrente de zero para 1 / L   ampéres?

Então, a gente viu que em t = 0 é aplicado um impulso de tensão de 3   V no indutor. Logo, esse impulso de 3   V vai alterar a corrente do indutor instantaneamente para 3 / 2 ampéres.

i L 0 = 3 2   A

Logo,

i L t = 3 2 e - 3 2 t   A

Passo 8

Agora que encontramos a corrente que passa pelo indutor para t > 0 , finalmente podemos encontrar o valor de v 0 t . Sabemos que:

v 0 t = 2 d i L d t

Substituindo,

v 0 t = 2 × d 3 2 e - 3 2 t   d t

v 0 t = 2 × - 9 4 e - 3 2 t

v 0 t = - 9 2 e - 3 2 t   u ( t )

Logo, a expressão geral para v 0 ( t ) quando a fonte de corrente é um degrau unitário é:

v 0 t = 3 δ t - 9 2 e - 3 2 t   u ( t )

Resposta

v 0 t = 3 e -   3 2 t   u t ,     p a r a   i 1 t = u ( t )

v 0 t = 3 δ t - 9 2 e - 3 2 t   u t ,     p a r a   i 1 t = δ t

Exercícios de Livros Relacionados

A questão quer que o aluno mostre que o resistor tem uma certa equação, e em seguida comparar com o resultado da questão anterior.
Essa questão é interessante, uma vez que se pode escolher qual configuração pode ser usada
Calcule i para t0 , se i (0) = 4 A e i_g = 8 A
O pulso na figura 7.116a pode ser expressa em termos de funções de singularidade como: a2 u t + 2 u t - 1V b2 u t - 2 u t - 1V c2 u t - 4 u t - 1V d2 u t + 4 u t - 1V
A constante de tempo para um circuito R L com R = 2 Ω e L = 4 H é:(a) 0,5 s (b) 2 s (c) 4 s (d) 8 s (e) 15 s