Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.Problemas - Ex. 21
10.21. Para o circuito fasorial mostrado, calcule Zeq e use o resultado para calcular o fasor corrente I. Se w = 2 rad/s, calcule a resposta forçada i correspondente a I.
Passo 1
Galera, tudo belezinha?
Primeiramente vamos recordar aqui do circuito da nossa questão.
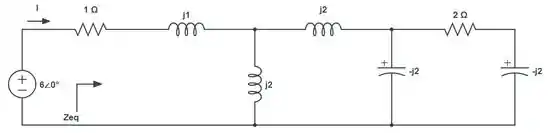
Vamos agora, calcular a resistência equivalente do circuito:
Agora, é possível, calcular a resposta forçada i correspondente a I:
Resposta
Exercícios de Livros Relacionados
Mostre que, no Prob. 15.6, se L = Q , C = 1 / Q e R = 1 , então H ( s ) = ( 1 / Q ) s s 2 + ( 1 / Q ) s + 1 que é uma função de rede passa-faixa com índice de mérito Q , freqüência central ω 0 =1 r a
Para o circuito mostrado, R = 2 Ω , L = 2 H e C = 0.02F . Se a entrada e a saida forem V 1 e V 2 , respectivamente, calcule a funçāo de rede e esboce as respostas em amplitude e fase. Mostre que o pic
Calcule H ( s ) = V 2 ( s ) / V 1 ( s ) e esboce as respostas em amplitude e fase. Mostre que o pico da amplitude e a fase zero ocorrem e m ω = 4 r a d / s .
Se R 1 = R 2 = 0,5 Ω e R 3 = 0,01 Ω no Prob. 15.4 , calcule H ( s ) . a frequência ω n na qual o pico da amplitude e a fase zero ocorrem e o módulo de H em ω 0
Altere em escala o circuito do Prob. 15.32 para obter um filtro passa-altas com ω t = 2000 r a d / s , usando capacitores de 0,05 μ F .