Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 8
Calcule a tensão para sobre um resistor de e um capacitor de em serie se a corrente e e o capacitor está descarregado em . Calcule o valor máximo da tensão e o menor valor de t para o qual ela ocorre.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Vamos primeiro anotar as variáveis, nós temos basicamente o seguinte para
A configuração está em série, com isso nós temos o seguinte circuito
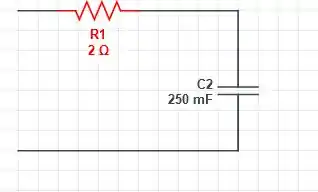
Agora, vamos analisar as tensões para cada componente, começando pelo resistor, que pela Lei de Ohm vamos ter a seguinte configuração
Logo, para o resistor de
Passo 2
Para o capacitor de nós temos que
Para resolver esta bela integral, temos que fazer pelo método da substituição, portanto
Logo, a integral será igual a
Agora, vamos entender o tempo máximo e a tensão máxima.
Passo 3
O menor valor de t para que se atinja a tensão máxima é igual a
Logo, para o caso de , nós temos que