Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 9

12.9. Calcule a potência média entregue ao resistor R, se R = 0,4 Ω.

Passo 1

Eai, tomou uma água, comeu um lanchinho? Respirou? Pois, vamos viajar em mais uma questão!

Vejamos! A questão nos pede pra calcular a potência média entregue ao resistor R , se R   =   0,4   Ω , do seguinte circuito:

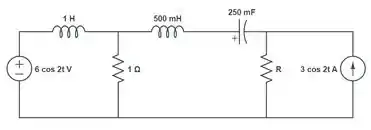
Equivalente a este circuito, podemos obter:

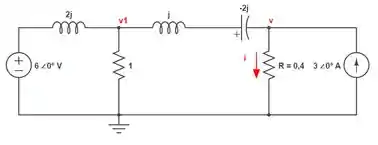
Sabendo que:

V = 6 cos ⁡ 2   t V

Temos:

6 - V 1 2 j = V 1 + V 1 - V - j

6 - V 1 2 j = j V 1 + V - V j

V 1 - 2 + 2 j + 2 V = 6 - V 1

2 V + V 1 - 1 + 2 j = 6

V 1 - V - j + 3 = V 0,4

V - V 1 + 3 j j = 10 V 4

4 V - 4 V 1 + 12 j = 10 j V

V ( 4 - 10 j ) - 4 V 1 = - 12 j

V = 6 - 1 + 2 j - 12 j - 4 2 - 1 + 2 j 4 - 10 j - 4 = - 48 - 12 j - 24 - 1 8 j = 1,65 ∠ - 22,83 °

Passo 2

Podemos então, determinar a corrente:

i = V 0,4 = 1,65 ∠ - 22,83 ° 0,4 = 4,123 ∠ - 22 , 8 3 °  

Logo, nossa Potência no resistor é calculada através da equação abaixo:

P R =   V m I m 2 c o s ⁡ ( V o - I o )

Agora, é só substituirmos os dados que já temos anteriormente:

P R =   1,65   .   4,123 2 c o s ⁡ ( 0 ° ) = 3,4   W

Resposta

P R =   3,4   W

Exercícios de Livros Relacionados

Calcule V e f i c a z .
Calcule os valores eficazes de (a) i = 10 s e n ω t + 20 cos ⁡ ( ω t + 30 ° ) , (b) i = 8 s e n ω t + 6 c o s ⁡ ( 2 ω t + 10 ° ) e (c) i = I 1 + cos ⁡ 377 t .
Calcule a potência média dissipada em um resistor de resistência R, se a corrente e i = I m ( 1 + cos ⁡ ω t ) .
Um ciclo de uma corrente periódica e dado por se a corrente flui em um resistor de 20Ω, calcule a potência media.
Um cicio de uma corrente peri6dica e como mostrado. Se a corrente flui em um resistor de 20Ω, calcule a potência media.