Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 14

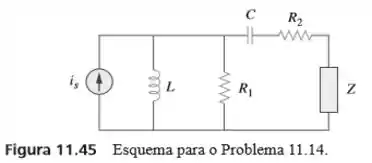
14. Elabore um problema para ajudar outros estudantes a entender melhor a máxima transferência de potência média. Considere a Figura 11.45.

Passo 1

O objetivo do problema é determinar Z para que ocorra a máxima transferência de potência média e o valor dessa potência.

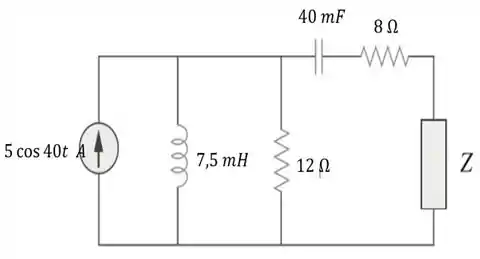
Como é um problema, cuja elaboração é de nossa responsabilidade, bora redesenhar o circuito atribuindo valores numéricos aos seus elementos.

Aqui está ...

E em seguida, bora passar os elementos pro domínio da frequência...

5 cos ⁡ 40 t   A → 5 ∠ 0 °       , ω = 40   r a d / s

40   m F → 1 j ω C = 1 j ⋅ 40 ⋅ 0,04 = - j 0,625   Ω

7,5   m H → j ω L = j ⋅ 40 ⋅ 0,0 075 = j 0,3   Ω

O nosso circuito passa a ter então, a seguinte cara:

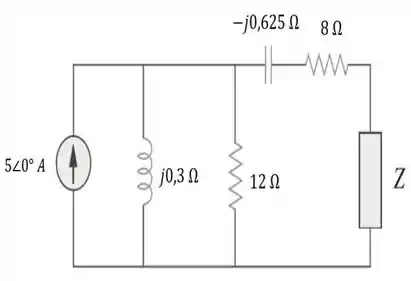
Esse é o circuito com o qual vamos trabalhar!

Passo 2

E pra facilitar a nossa vida, bora tratar de encontrar a impedância de T h é v e n i n desse circuito, que vai estar conectada a impedância Z .

Para isso, bora substituir aquela fonte de corrente por um circuito aberto e tirar o Z , afinal o objetivo é encontrar uma impedância ligada em série com Z , que é a Z T h .

Desse jeito aqui...

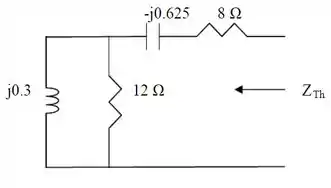
Por essa figura, podemos ver que a impedância de T h é v e n i n , Z T h , é dada por...

Z T h = j 0,3 | | 12 - j 0,625 + 8   Ω

Z T h = j 0,3 ⋅ 12 j 0,3 + 12 - j 0,625 + 8   Ω

Z T h = 8,0075 - j 0,3252   Ω

Para que ocorra a máxima transferência de potência, Z precisa ser igual ao conjugado de Z T h , ou seja...

Z = 8,0075 + j 0,3252   Ω

Pronto! Já temos uma resposta!

Passo 3

Em seguida, vamos tratar de determinar a tensão de T h é v e n i n , V T h , pra esse circuito.

Assim, bora fazer um desenho pra ver de que jeito vamos fazer isso...

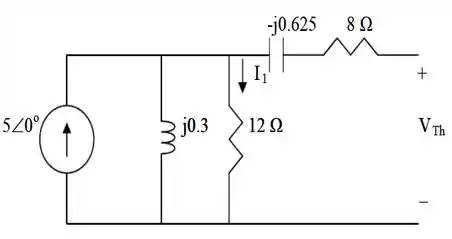
O melhor jeito de se determinar V T h , é determinar a corrente I 1 que está circulando no resistor de 12   Ω .

E podemos fazer isso, usando a divisão de corrente. Do seguinte jeito...

I 1 = j 0,3 12 + j 0,3 ⋅ 5 ∠ 0 °   A

I 1 = 1,5 ∠ 90 ° 12,004 ∠ 1,43 °   A

I 1 = 0,12496 ∠ 88,57 °   A

I 1 = 0,003118 + j 0,12492   A

Desse modo, a tensão de T h é v e n i n   ( R M S ) é igual...

V T h , R M S = 12 ⋅ 0,12496 ∠ 88,57 ° 2

V T h , R M S = 1,0603 ∠ 88,57 °   V

Como o objetivo é determinar a máxima potência média; para determinar a corrente R M S média basta dividir a tensão de T h é v e n i n   R M S pela parte real da impedância Z vezes 2 .

I R M S = V T h , R M S ( Z T h + Z )

I R M S = 1,0603 ∠ 88,57 °   V 2 ⋅ 8,008   Ω

I R M S = 66,2 ∠ 88,57 °   m A

E a potência média vai ser expressa por...

P m e d = ( 8,0075   Ω ) ⋅ ( 66,2 ∠ 88,57 °   m A ) 2

P m e d = 35 , 0 9   m W

Encontramos a outra resposta!

Resposta

Z = 8,0075 + j 0,3252   Ω

P m e d = 35 , 0 9   m W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7. Dado o circuito da figura 11.39 , determine a potência média absorvida pelo resistor de 10Ω .
11. Para o circuito da figura 11.43 , suponha que a impedância da porta seja: Z = R 1 + ω 2 R 2 C 2 ∠ - tan - 1 ⁡ ω R C Determine a potência média consumida pelo circuito quando R = 10k Ω , C = 200n F
17. Calcule o valor de Z L no circuito da figura 11.48 de modo que Z L receba a máxima potência média. Qual é a máxima potência média recebida por Z L ?
18. Determine o valor de Z L no circuito da figura 11.49 abaixo para a transferência de potência máxima.
19. O resistor variável R no circuito da figura 11.50 é ajustado até ele absorver a máxima potência média. Determine R e a máxima potência média absorvida.