Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 15
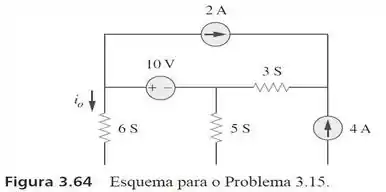
15. Aplique análise nodal para determinar e a potência dissipada em cada resistor no circuito da Figura
Passo 1
Bom! A primeira coisa que devemos saber antes de resolver essa questão é que a corrente elétrica irá sempre se deslocar de um ponto de maior potencial pra um de menor potencial.
E a segunda coisa que temos que fazer é de dar nomes aos bois. Essa figura tá meio vazia, né não? Precisa de um toque de classe, não concorda!?
Tá faltando colocar o sentido das correntes, os nós, atribuir variáveis às tensões nodais, etc.
Por isso, o que devemos fazer é dar uma embelezada nesse circuito de forma que ele possa estar mais compreensível para realizarmos a nossa análise nodal. Vamos lá! Aqui está nossa obra prima...
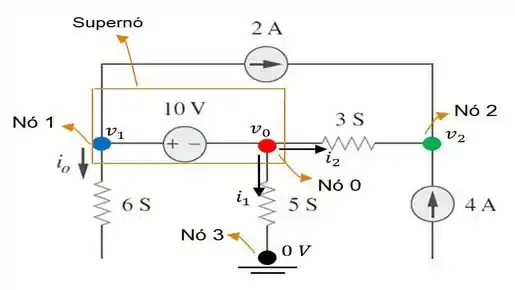
Olha só! Você aí deve estar se perguntando! Que raios é esse nas resistências de nossa figura? Não deveria ser ?
Calma que eu vou explicar! A resistência em nada mais é do queo inverso da resistência em . Se temos então uma resistência de , é porque a resistência equivalente em é:
A resistência em é muito útil. Ao invés de dividirmos a tensão nodal pela resistência equivalente em ... Quando a resistência está em , iremos multiplicar a tensão nodal pela resistência.
Passo 2
Nosso circuito possui nós, sendo que o nó de número está ligado à terra e portanto, possui potencial nulo.
E podemos ver que no nosso circuito, há a presença de um supernó. Sendo assim, aplicando a para ele, temos que:
E depois, aplicando a para o nó , chegamos à:
Uma vez que a corrente sai sempre do maior para o menor potencial, vamos determinar agora as equações das correntes em relação às tensões em cada resistor:
E substituindo em seguida essas fórmulas, nas duas relações que obtivemos do , chegamos ao seguinte sistema de equações:
Passo 3
Agora, bora dar uma ajeitadinha nesse sistema:
Vamos isolar na equação :
E substituir essa relação em :
Só que do supernó, tiramos que:
O que nos faz ficar com:
E consequentemente, é dada por:
E , por:
Passo 4
Por fim, para obter basta usar:
Quanto às potência dissipadas em cada resistor! Olha só! Pro caso específico em que a resistência está em e não em , a potência é dada por:
Desse modo, obtemos os seguintes resultados: