Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 16

16. No circuito da Figura 11.46, determine o valor de Z L , que absorverá a potência máxima, e o valor da potência máxima.

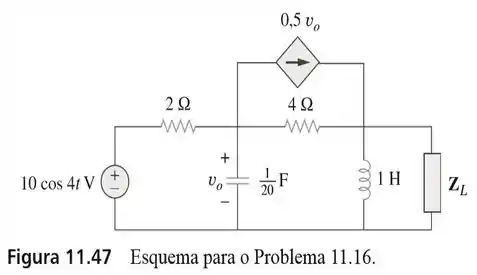
Passo 1

Primeiramente, vamos passar todos os elementos desse circuito pro domínio da frequência...

10 cos ⁡ 4 t   V → 10 ∠ 0 °       , ω = 4   r a d / s

1 20   F → 1 j ω C = 1 j ⋅ 4 ⋅ 1 20 = - j 5   Ω

1   H → j ω L = j ⋅ 4 ⋅ 1 = j 4   Ω

Feito isso! Vamos tentar encontrar a impedância de T h é v e n i n desse circuito.

Para isso, bora substituir a fonte de tensão de 10 cos ⁡ 4 t   V por um curto circuito e trocar Z L por uma fonte de corrente de 1   A . Na prática, o que estamos fazendo aqui é usando o princípio da linearidade

Vamos aproveitar a deixa e preparar também o circuito pra receber a análise nodal...

Aqui está...

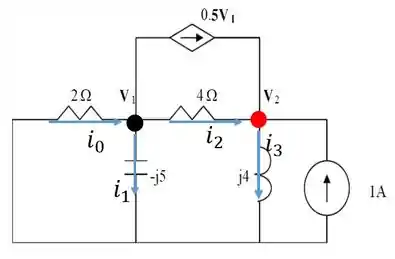
Em seguida, bora fazer a L K C para o nó 1 , já substituindo pelas tensões nodais correspondentes...

i 0 = i 1 + i 2 + 0,5 V 1

- V 1 2 = V 1 - j 5 + V 1 - V 2 4 + 0,5 V 1

- 0,5 V 1 = j 0,2 V 1 + 0,25 V 1 - 0,25 V 2 + 0,5 V 1

V 1 1,25 + j 0,2 - 0,25 V 2 = 0   ( i )

Fazendo a mesma coisa para o nó 2 :

i 2 + 1 + 0,5 V 1 = i 3

1 + V 1 - V 2 4 + 0,5 V 1 = V 2 j 4

- 1 = 0,75 V 1 + V 2 - 0,25 + j 0,25   ( i i )

Temos então, o seguinte sistema linear com duas equações:

V 1 1,25 + j 0,2 - 0,25 V 2 = 0   ( i ) 0,75 V 1 + V 2 - 0,25 + j 0,25 = - 1   ( i i )

Isolando V 1 em ( i ) :

V 1 1,25 + j 0,2 - 0,25 V 2 = 0

V 1 = 0,25 1,25 + j 0,2 V 2

E depois substituindo em ( i i ) :

0,75 V 1 + V 2 - 0,25 + j 0,25 = - 1

0,1875 1,25 + j 0,2 V 2 + V 2 - 0,25 + j 0,25 = - 1

0,146 V 2 - j 0,0234 V 2 + V 2 - 0,25 + j 0,25 = - 1

V 2 = - 1 - 0,104 + j 0,227

V 2 = 1 ∠ 180 ° 0,249 ∠ 114,615 °

V 2 = 1,67 + j 3,6 5   V

E como podemos ver no circuito anterior, a impedância de T h é v e n i n   vai ser dada por...

Z T h = V 2 1

Z T h = 1,67 + j 3,65   Ω

Z T h = 4,01 6 ∠ 6 5 , 38 °   Ω

A impedância Z L vai ser o conjugado de Z T h , ou seja...

Z L = 4,01 6 ∠ - 6 5 , 38 °   Ω

Passo 2

Em seguida, vamos tratar de determinar a tensão de T h é v e n i n , V T h , pra esse circuito.

Assim, bora fazer um desenho pra ver de que jeito vamos fazer isso...

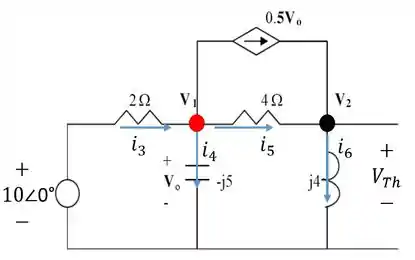
Fazendo a análise nodal pra esse nó destacado de vermelho, temos que:

i 3 = i 4 + i 5 + 0,5 V 0

Como V 1 = V 0 ;

10 - V 1 2 = V 1 - j 5 + V 1 - V 2 4 + 0,5 V 1

V 1 1,25 + j 0,2 - 0,25 V 2 = 5  

Em seguida, fazendo a análise nodal pro nó destacado de preto...

i 5 + 0,5 V 0 = i 6

V 1 - V 2 4 + 0,5 V 1 = V 2 j 4

0,75 V 1 + V 2 - 0,25 + j 0,25 = 0

Temos então, o seguinte sistema linear com duas equações:

V 1 1,25 + j 0,2 - 0,25 V 2 = 5   ( i i i ) 0,75 V 1 + V 2 - 0,25 + j 0,25 = 0   ( i v )

Isolando V 1 em ( i v ) :

0,75 V 1 = V 2 0,25 - j 0,25

V 1 = 0,25 - j 0,25 0,75 V 2

E depois substituindo em ( i i i ) :

1 - j 1 3 1,25 + j 0,2 V 2 - 0,25 V 2 = 5

2 ∠ - 45 ° 3 1,2659 ∠ 9,09 ° V 2 - 0,25 V 2 = 5

( 0 , 233 - j 0 , 3 5 ) V 2 = 5

V 2 = 5 0,233 - j 0,35

V 2 = 6,59 + j 8,89   V

Essa tentão V 2 , como podemos ver no circuito da figura no começo desse P a s s o , é a nossa tensão de T h é v e n i n . Sendo assim...

V T h = 6,59 + j 8,89   V

Passo 3

Obtido o valor da impedância Z L e da tensão V T h , para encontrar a máxima potência média basta usar a fórmula abaixo:

P m e d = 1 2 V T h Z T h + Z L 2 ⋅ R T h

Onde R T h é a parte real de Z T h .

Substituindo assim, os valores numéricos:

P m e d = 1 2 6,59 + j 8,89   1,67 + j 3,65 + 1,67 - j 3,65   2 ⋅ ( 1,67 )

P m e d = 1 2 6,59 + j 8,89   3,34 2 ⋅ ( 1,67 )

P m e d = 1 2 11 , 89 ∠ 56,35 ° 3,34   2 ⋅ ( 1,67 )

P m e d = 10,5817   W

Resposta

Z L = 4,016 ∠ - 65,38 °   Ω

P m e d = 10,5817   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12. Para o circuito abaixo, determine a impedância Z L da carga para a transferência da potência máxima ( para Z ) . Calcule a potência máxima absorvida pela carga.
14. Elabore um problema para ajudar outros estudantes a entender melhor a máxima transferência de potência média. Considere a Figura 11.45.
15. No circuito da Figura 11.46, determine o valor de Z L , que absorverá a potência máxima, e o valor da potência máxima.
20. A resistência de carga R L na Figura 11.51 é ajustada até ela absorver a máxima potência média. Calcule o valor de R L e a máxima potência média.