Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 23

23. Elabore um problema para ajudar outros estudantes a entenderem melhor como determinar o valor R M S de uma forma de onda. Usando a figura 11.54

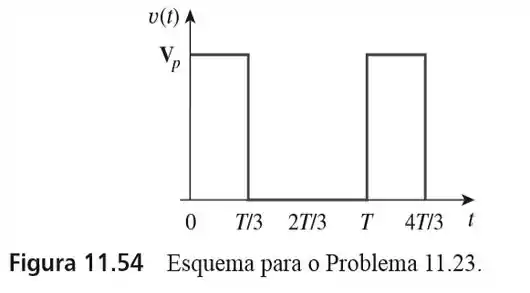
Passo 1

Olha só! Como é uma questão que nós vamos ter que elaborar, bora redesenhar o circuito atribuindo valores a cada uma das variáveis.

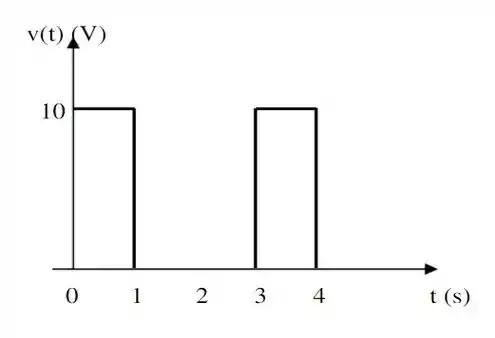
Passo 2

E a tensão R M S , é dada, usando a fórmula abaixo, por:

V R M S = 1 T ∫ 0 T v 2 ( t ) d t

O período da nossa onda é 3 ! Só que do instante 0   ao 3 , nossa função de onda é dada por:

v t = 10 ,       0 < t < 1 v t = 0 ,       1 < t < 2

Assim, nossa integral fica com a seguinte cara...

V R M S = 1 T ∫ 0 T v 2 ( t ) d t

V R M S = 1 3 ∫ 0 1 10 2 d t

V R M S = 1 3 ∫ 0 1 100 d t

V R M S = 100 3

V R M S = 5,7735   V

Resposta

V R M S = 5,7735   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3. Uma carga é formada por um resistor de 60Ω em paralelo com um capacitor de 90m F . Se a carga for conectada a uma fonte de tensão v s t = 160 cos ⁡ 2000 t , determine a potência média liberada para
2. Dado o circuito da Figura 11.35 , determine a potência média fornecida ou absorvida por cada elemento.
27. Calcule o valor R M S da forma de onda de corrente da figura 11.58
13. A impedância de T h é v e n i n é de uma fonte é Z T h = 120 + j 60Ω , enquanto a tensão de T h é v e n i n é de pico é V T h = 165 + j 0 V . Determine a potência máxima disponível da fonte.
22. Determine o menor valor R M S da onda senoidal deslocada abaixo: