Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 20
20. A resistência de carga na Figura 11.51 é ajustada até ela absorver a máxima potência média. Calcule o valor de e a máxima potência média.
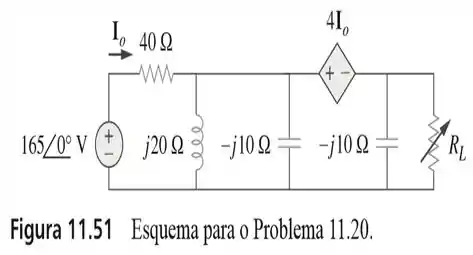
Passo 1
Olha só! No nosso circuito, vemos que as impedâncias de e estão em paralelo. A impedância equivalente nesse caso, vai ser igual a...
Em seguida, vamos nos concentrar em obter a impedância de . Para isso, vamos substituir aquela resistência ali por uma fonte de corrente de . Quanto a fonte de tensão, nós vamos trocar por um curto circuito, como é de praxe.
Aproveitando a deixa, bora indicar o sentido das correntes, né? Tá na cara que vamos precisar fazer uso da análise nodal mais uma vez.
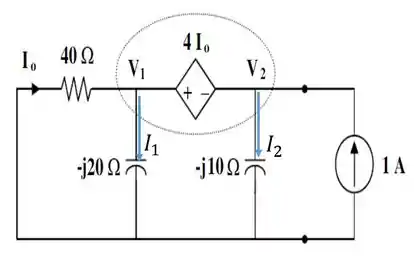
Essa região envolta por uma elipse pontilhada aí, é um supernó. Bora aplicar a pra ele...
Só que do supernó...
Mas...
O que nos leva à...
Substituindo essa relação em :
E consequentemente,
Calculando a impedância de , em seguida...
O que fizemos foi dividir a fonte de tensão pela fonte de corrente de , de modo que...
Como nosso elemento é uma resistência, ou seja, só tem parte real presente... Então, a resistência vai ser igual ao módulo de ...
Passo 2
Agora, vamos nos concentrar em obter o valor de .
Para isso, bora redesenhar o circuito, abrindo ele no ramo que contém .
Desse jeito aqui...
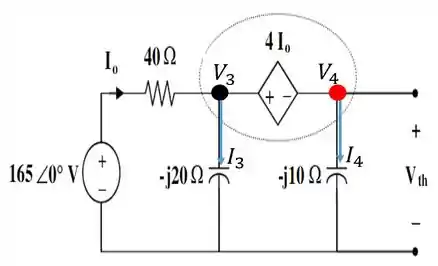
Essa região envolta por uma elipse pontilhada aí, é um supernó. Bora aplicar a pra ele...
Só que do supernó...
Mas...
O que nos leva à...
Substituindo essa relação em :
Desse modo...
Essa , como podemos ver no nosso circuito é a nossa tensão de ....
Passo 3
Obtido o valor da impedância e da tensão , para encontrar a máxima potência média basta usar a fórmula abaixo:
Onde é a parte real de .
Substituindo assim, os valores numéricos: